プロセス工学数学B
Takuya Kawanishi
◀ Previous TOC Next ▶

多変数関数の極大・極小

はじめに

最大・最小問題, あるいは極大・極小問題は多くの分野に現れる. 多くの産業で, 費用やエネルギーを最小にするための試みは日常的に行われているし, また, 機械学習では計算の大半が何らかの極小値を求めるのに費やされている.

1変数の連続関数の極大値・極小値については, 高校数学で習うように, その関数の導関数を調べれば分かる. これに比べて, 多変数関数の極大・極小問題は少し難しくなる. しかし, これは, 大学の 1 年生で学んだ微分積分学と線形代数学の知識を使うことで, 見通しよく解けるのである.

本章では, 2 変数関数の極大・極小問題を例として多変数関数の極大・極小問題の解き方を学ぶ. 本章で学ぶ事項は, 広く使われている「最適化手法」の基礎をなすものである.

なお, この章では, 実行列のみを扱う. 応用上重要な極大・極小問題のほとんどは実行列で表現できると考えられるためである.

極大・極小問題とは

1変数関数の極大極小

まずは, 1 変数関数の場合の復習から始めよう. fig: local max and local min of one variable function は, 関数

\[y = f(x) = x^3 - 3 x\]

をプロットしたものである.

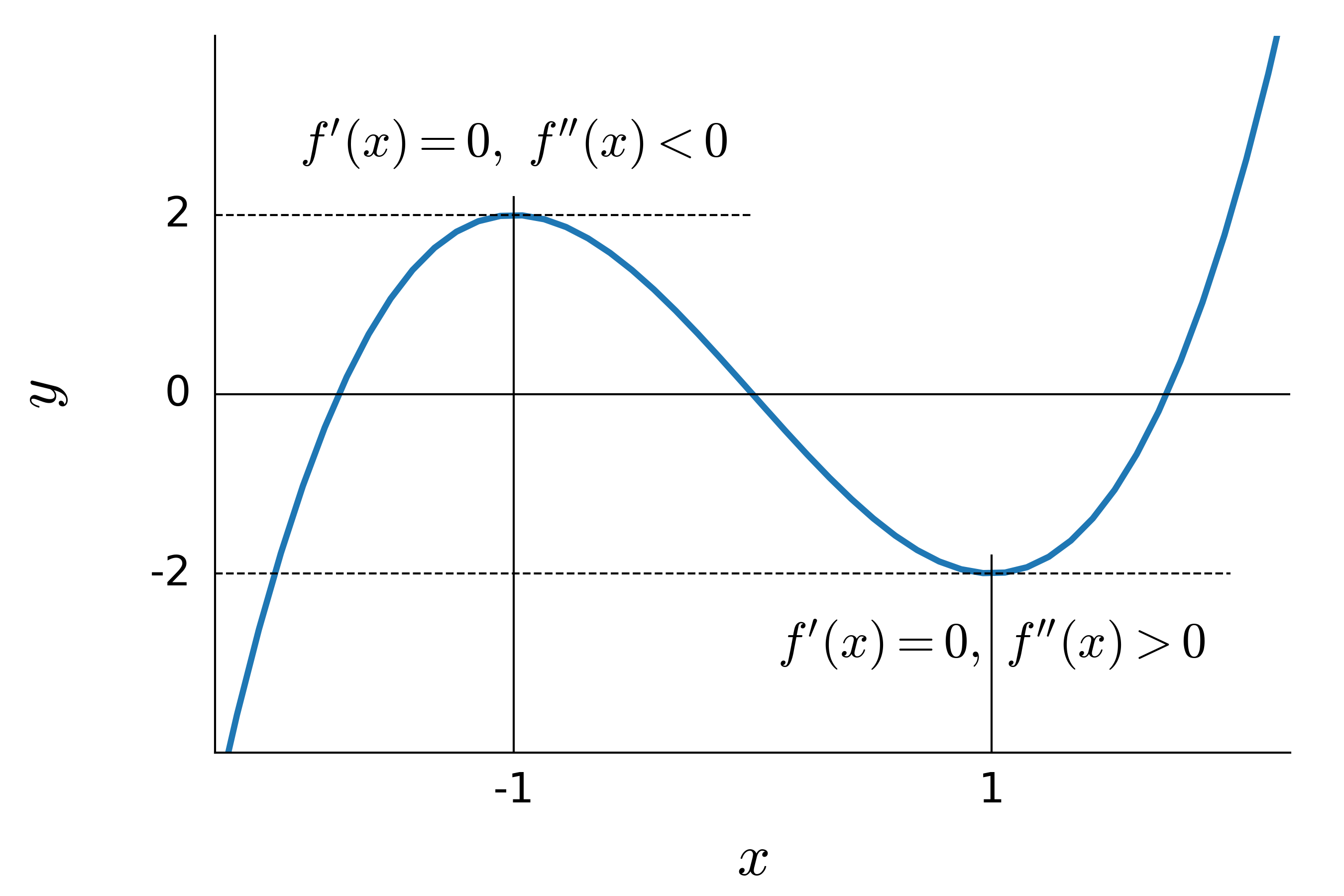
../_images/one_variable_local_max.png

この関数は \(x = -1\) で極大値, \(x = 1\) で極小値をもつ. つまり \(x = -1\) と \(x=1\) はそれぞれこの関数の極大点, 極小点だが, この2つの点は\(f^\prime(x) = 3 x ^2 - 3 =0\) の解になっており, \(f^{\prime\prime}(-1) = 6x\vert_{x=-1} = -6 < 0\) より前者が極大値, \(f^{\prime\prime}(1) = 6x\vert_{x=1}= 6 > 0\) より, 後者が極小値を与えることが分かる. すなわち, 極値を与えるかもしれない \(x\) は, \(f^\prime(x) = 0\) の解（停留点という）であり, その点で \(f^{\prime\prime}(x)\) の値が正であればその点が極小点, 負であれば極大点である. もし \(f^{\prime\prime}(x) = 0\) ならば, 極大極小を調べるには, さらに \(f^{(3)}(x)\) などを調べる必要があるが, 1 変数関数の場合, その導関数を調べることにより, 極大点・極小点を求めることができるわけである.

2変数関数の場合の例

では, 2 変数関数の場合はどうだろうか. 例として,

\[z=f(x, y)=\frac{1}{4}x^2+\frac{1}{4}y^2+xy\]

を考えてみよう.この関数は, \(x=0\) 平面, \(y=0\) 平面上ではそれぞれ

\[z = f(0, y) = \frac{1}{4} x^2 , \quad z = f(x, 0) = \frac{1}{4} x^2\]

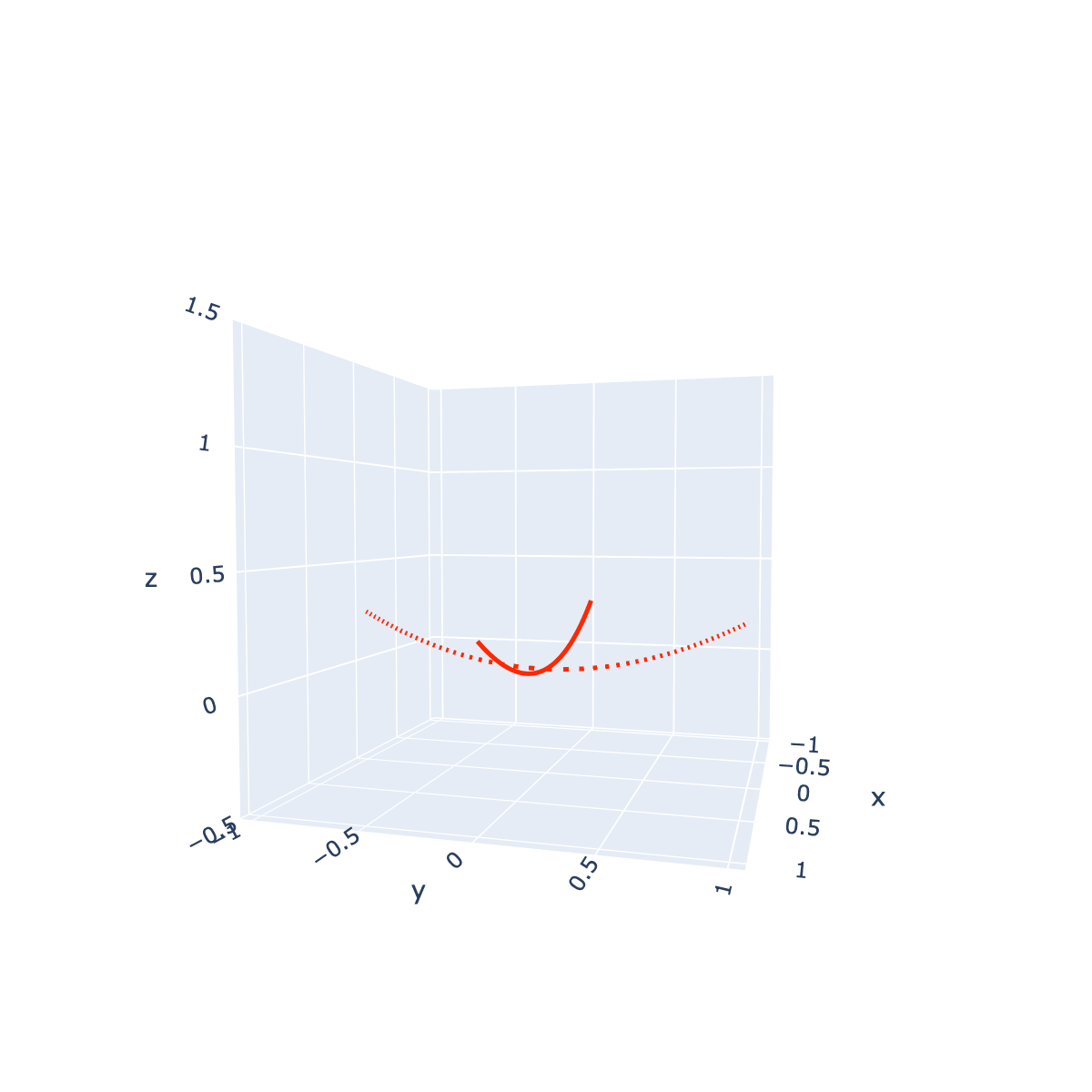
である. この 2 つの平面での値を 3D の線図に示すと fig: two variables 3D line x=0, y=0 のようになる. つまり, \(x=0\) 平面上と \(y=0\) 平面上の値に限っては, この関数は \(x=y=0\) で極小値を持っている. では, \((x, y) = (0, 0)\) は極小点なのだろうか.

../_images/local_minmax_2var_3d_x_y_planes_lines.png

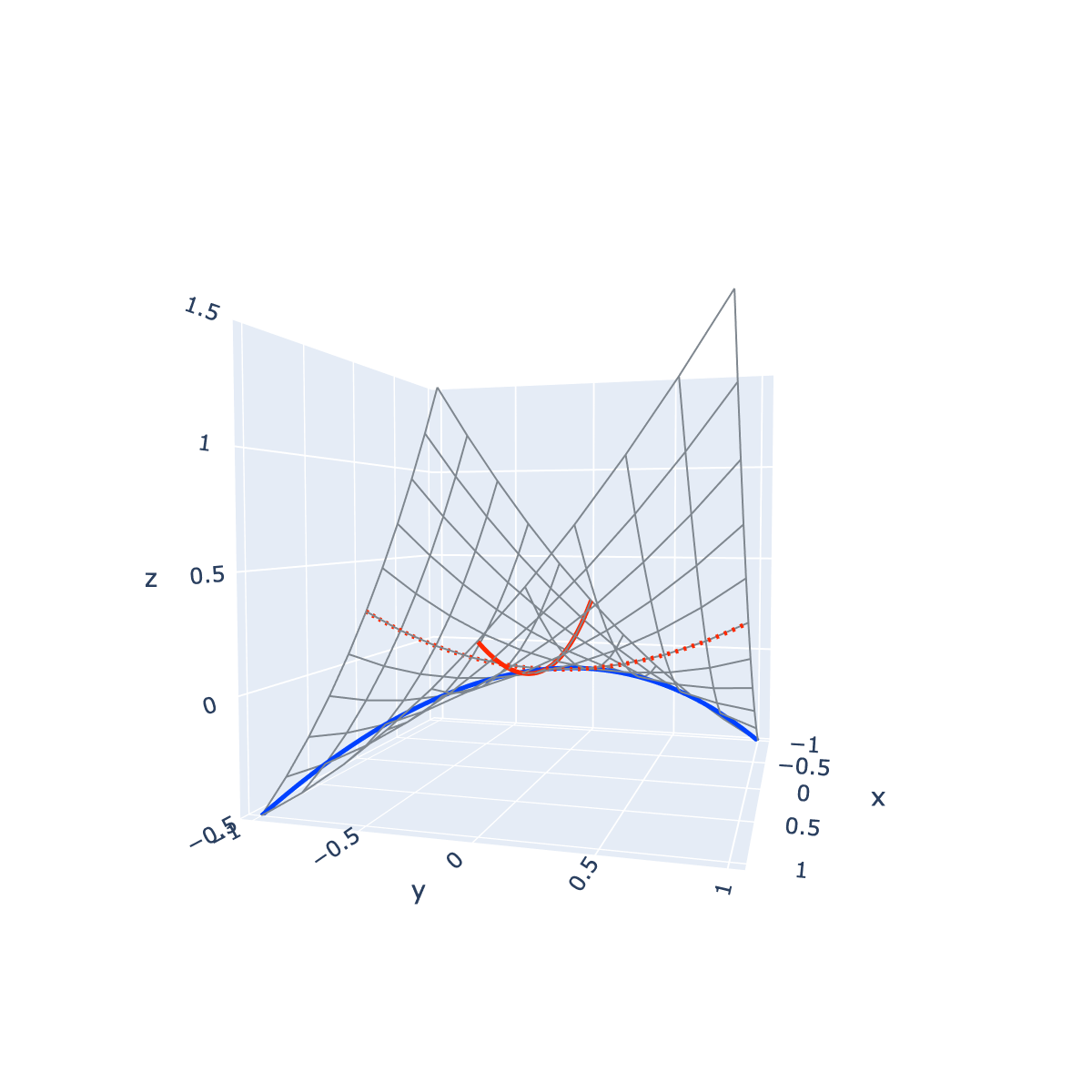
答えを先に言ってしまえば, \((x, y)=(0, 0)\) はこの関数 \(z=f(x, y)\) の極小値ではない. 3D グラフで見ると, \(z = \frac{1}{4}x^2 + \frac{1}{4}y^2 + xy\) はfig: two variables 3D line x=0, y=0 のようになっている. 先ほど見たように, \(x=0\) 平面, \(y=0\) 平面では, 関数の値は \((x, y)=0\) で極小となっている. しかし, \(y=-x\) 平面では, 図から分かるように, 関数の値は上に凸になっており, \((x, y)=(0, 0)\) で極大値となっている. よって, \((x, y)\) はこの関数の極小点ではないのである. 因みにこの点 \((x, y)=(0, 0)\) のように, ある方向に沿った場合は極小値で, ある方向に沿った場合は極大値であるような点を鞍点 (saddle point)という.

../_images/local_minmax_2var_3d_wireframe.png

多変数関数の極大・極小問題の難しさ

あらためて 2 変数の場合の難しさを考えてみよう. 先ほどの例では, \(z\) 軸に平行な面のうち, 面 \(x=0\), 面 \(y=0\) では, \(z=f(x, y)\) のグラフは \((x, y)=(0, 0)\) で極小値をとるが, 面 \(y=-x\) では \((x, y)=(0, 0)\) で極大値をとった.

関数 \(z=f(x, y)\) が \((x, y)=(0, 0)\) で極小値をとるためには, \(x=0\), \(y=0\), \(y=-x\) を含む, \(z\) 軸を含むあらゆる面で（方向としては, \(360^\circ\) （\(180^\circ\)？）あらゆる方向で）その面の中の関数のグラフが極小値をとらなければならない. これが, 1変数の場合との違いである. いわば, 2変数の場合は, 問題の質が違っているのである. では, どうすれば良いのだろうか？ 実は, 2 変数を含め, \(n\) 変数 \((n \ge 2\) の場合の極大・極小問題は, これから述べる方法によって, 全て同じ手順で解けるのである. 次節では, まず, この方法を説明し, そのあとに, なぜその方法で解けるのかを解説しよう.

2変数関数の極大・極小問題

極点, 極値を求める手順

手順 1.1 (2変数関数 \(z=f(x, y)\) の極点, 極値を求める手順)

  1. 2変数関数 \(f:\mathbb R^2\to \mathbb R\) は2回連続微分可能であると仮定する [1].

  2. \(z = f(x, y)\) の停留点 (stationary point) をすべて求める.

  3. 各停留点において, Hesse 行列 (Hessian matrix) を求める.

  4. 上で求めた Hesse 行列の固有値を求める.

  5. Hesse 行列の固有値がすべて正ならば, その点は極小値, すべて負ならば, その点は極大値, もし正と負であれば, その点は鞍点である. 固有値が 0 を含む場合, さらに高階の導関数を調べる必要がある.

2変数関数の Taylor 展開と極小点

2変数あるいはそれ以上の多変数関数の極大・極小問題では, Hesse 行列（とその固有値）を用いる. これが1変数の場合との大きな違いとなる. ここでは, 極大・極小問題と Hesse 行列をつなぐために, Taylor 展開を用いる. Taylor 展開は, 大学の1年生で学ぶが, 高次項や剰余項の取扱など面倒に思ったかもしれない. しかし, 応用では, たいてい1次までの近似で十分（まれに2次まで）であり, 剰余項はたいてい無視するので実はさほど面倒ではない. なので, 積極的に手を動かして計算をしてみて欲しい. まずは, 2回連続微分可能な2変数関数 \(z = f(x, y)\) の Taylor 展開を下に示そう. 剰余項は \(R\) で示す. (1) 1 次までの展開

\[\begin{split}\begin{aligned} &f(x + \Delta x, y + \Delta y) \\ \quad &= f(x, y) + \frac{\partial f}{\partial x}(x, y) \Delta x + \frac{\partial f}{\partial y}(x, y) \Delta y + R\end{aligned}\end{split}\]

  1. 2 次までの展開

(1)\[\begin{split}\begin{aligned} &f(x + \Delta x, y + \Delta y) = f(x, y) + \frac{\partial f}{\partial x} (x, y) \Delta x + \frac{\partial f}{\partial y} (x, y) \Delta y \notag\\ & \quad + \frac{1}{2} \left\{\frac{\partial^2 f}{\partial x^2}(x, y) (\Delta x)^2+ 2\frac{\partial^2 f}{\partial x \partial y}(x, y) \Delta x \Delta y+ \frac{\partial^2 f}{\partial y^2}(x, y) (\Delta y)^2 \right\} + R \label{eq: expansion of f to second order}\end{aligned}\end{split}\]

ここに示した展開では, \(\partial^2 f / \partial x \partial y = \partial^2f /\partial y \partial x\) を用いている. これを用いることは, 次の 定理 1.2 と 例題 1.1 で正当化される.

定理 1.2

\(\partial^2 f / \partial x \partial y\) と \(\partial^2 f / \partial y \partial x\) が存在し, かつ, ともに \((x, y) = (a, b)\) において連続であることが十分である.

(2)\[\frac{\partial^2 f}{\partial x \partial y}(a, b) = \frac{\partial^2 f}{\partial y \partial x}(a, b) \qquad \Box \label{eq: exchange order partial differentiation}\]

証明は微積分学の教科書などを参照していただきたい.

例題 1.1

を含むある開領域で 2 回連続微分可能であれば, 式 (2) が成立することを示せ.

解答例題 1.1 . 関数が \(z = f(x, y)\) が 2 回連続微分可能ということは, \(f\) の2階導関数, すなわち次の 4 つの関数がすべてが存在して, かつ連続であるということである.

\[\frac{\partial^2 f}{\partial x^2}, \quad \frac{\partial^2 f}{\partial x \partial y},\quad \frac{\partial^2 f}{\partial y \partial x}, \quad \frac{\partial^2 f}{\partial y^2}\]

したがって, 定理 1.2 より, (2) が成り立つ.

備考 1.3

例題 1.1 の \((a, b)\) を含む開領域で, という条件だが, もし領域が閉領域だと, その境界上の点での微分の定義が少々面倒になる. 例えば, 1 次元の閉区間の端点では, 右連続, 左連続の概念が必要になる. 開領域では境界上の点がなく, 特別なことを考えなくてすむのである.

定義 1.4

点 \((a, b)\) が関数 \(f(x, y)\) の停留点であるとは,

\[\frac{\partial f}{\partial x}(a, b) = 0, \quad \frac{\partial f}{\partial y}(a, b)=0\]

が成り立つことである.

\(\boldsymbol a = [a_1, \dotsc, a_n]^{\mathrm T}\) が \(n\) 変数関数 \(f(\boldsymbol x) = f(x_1, \dotsc, x_n)\) の停留点であるとは,

\[\frac{\partial f}{\partial x_i}(\boldsymbol a) = 0, \quad (i=1, \dotsc, n)\]

が（すべての \(i\) について）成り立つことである.

定理 1.5 (極小値をとるための条件)

2回連続微分可能な関数 \(z=f(x, y)\) が \((x, y) = (a, b)\)で極小値をとるためには, 次の2つの条件が成立することが十分である.

条件 1（停留点）

\[\frac{\partial f}{\partial x}(a, b) = 0, \quad \frac{\partial f}{\partial y}(a, b) = 0\]

条件 2（正値性） \(\Delta x \ne 0\) または \(\Delta y \ne 0\) に対して

\[\frac{\partial^2 f}{\partial x^2}(a, b) (\Delta x)^2 + 2\frac{\partial^2 f}{\partial x \partial y}(a, b) \Delta x \Delta y + \frac{\partial^2 f}{\partial y^2}(a, b) (\Delta y)^2 > 0. \qquad \Box\]

Proof. \(\ \)\(f(x, y)\) の2次までの展開 (1) 式において, \((x,y)=(a,b)\) とおく.

(3)\[\begin{split}\begin{aligned} &f(a+ \Delta x, b+ \Delta y) = f(a, b) + \underline{\frac{\partial f}{\partial x} (a, b) \Delta x + \frac{\partial f}{\partial y} (a, b) \Delta y} \notag\\ & \quad + \underline{\underline{\frac{1}{2} \left\{\frac{\partial^2 f}{\partial x^2}(a, b) (\Delta x)^2+ 2\frac{\partial^2 f}{\partial x \partial y}(a, b) \Delta x \Delta y+ \frac{\partial^2 f}{\partial y^2}(a, b) (\Delta y)^2 \right\}}} + R \label{eq: expansion of f to second order at (a, b)}\end{aligned}\end{split}\]

条件1により, 右辺第2項, 第3項（\(\mathrm{RHS}_{23}\) とおく）は

\[\underline{\mathrm{RHS}_{23} = \frac{\partial f}{\partial x}(a, b) \Delta x + \frac{\partial f}{\partial y} (a, b) \Delta y} =0\]

となる. また, 条件2により, 右辺第4項（\(\mathrm{RHS}_4\) とおく）は \(\Delta x \ne 0\) または \(\Delta y \ne 0\) のもとで

\[\underline{\underline{\mathrm{RHS}_4 = \frac{1}{2} \left\{\frac{\partial^2 f}{\partial x^2}(a, b) (\Delta x)^2+ 2\frac{\partial^2 f}{\partial x \partial y}(a,b) \Delta x \Delta y+ \frac{\partial^2 f}{\partial y^2}(x, y) (\Delta y)^2 \right\}}} > 0.\]

さらに, \(\Delta x\), \(\Delta y\) の絶対値が十分小さければ, 剰余項の絶対値は \(\mathrm{RHS}_4\) の絶対値よりも小さくなる. つまり, \(\mathrm{RHS}_4 + R >0\) である. 以上より

\[\underline{\mathrm{RHS}_{23}} + \underline{\underline{\mathrm{RHS}_4}} + R > 0\]

すなわち

\[f(a + \Delta x, b + \Delta y) - f(a, b) =\underline{\mathrm{RHS}_{23}} + \underline{\underline{\mathrm{RHS}_4}} + R > 0.\]

これは, \((x, y)\) が \((a, b)\) からどのような方向に変化 \((\Delta x, \Delta y)\) したとしても,（\(\Delta x \ne 0\) または \(\Delta y \ne 0\) である限り）\(f(a + \Delta x, b + \Delta y)\) の値は \(f(a, b)\) の値よりも大きくなること, すなわち \((a, b)\) が極小点であることを示している. ◻

備考 1.6

2変数の場合は, 2次関数の判別式を用いても解ける. しかし, この方法は3変数以上の場合には使えないのでここでは扱わない.

2次形式とHesse 行列 (Hessian matrix)

さて, 定理 1.5 (極小値をとるための条件) の条件 2 は, Hesse 行列 \(H\)（あとで定義する）を用いると次のようになる.

任意の \(\boldsymbol x \in \mathbb R^2\), \(\boldsymbol x \ne \boldsymbol 0\) に対して

(4)\[\boldsymbol x^\mathrm T H \boldsymbol x > 0 \label{eq: quadratic form of hessian}\]

ここで \(\boldsymbol x^\mathrm T\) はベクトル \(\boldsymbol x\) の転置 (transpose) を表す [2].式 (4) の左辺は \(\boldsymbol x ^{\mathrm T} A \boldsymbol x\) の形をしているが, 一般に, 対称行列 \(A\) に対し, \(\boldsymbol x^\mathrm T A \boldsymbol x\) を2次形式（あるいは2次形式の行列表現）という.

定義 1.7

2変数関数の2次形式とは

(5)\[Q(x, y) = a x^2 + b xy + c y^2 \label{eq: def quadratic form 2nd order}\]

で, \(a, b, c\) のうち少なくともひとつは \(0\) でないものをいう.

備考 1.8

\(n\) 変数の2次形式は次のように定義できる.

\[Q(x_1, \dotsc, x_n) = \sum_{i, j=1}^n a_{ij} x_i x_j \quad \text{少なくともひと組の } (i, j) \text{ について } a_{ij} \ne 0\]

命題 1.9

2次形式は対称行列により表現できる.

Proof. 　ここでは2変数の場合のみについて示す（3変数以上も同様に示すことができる）. \(\boldsymbol x=[x, y]^\mathrm T\), 対称行列を

\[\begin{split}S = \begin{bmatrix} a & \frac{1}{2} b \\ \frac{1}{2} b & c \end{bmatrix}\end{split}\]

とおくと

\[\begin{split}\boldsymbol x^\mathrm T S \boldsymbol x = \left[ x, y\right] \begin{bmatrix} a & \frac{1}{2} b \\ \frac{1}{2} b & c \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}= a x^2 + b xy + c y^2\end{split}\]

つまり, 任意の2次形式 (5) について, 上記の対称行列\(S\) を取れば, \(Q(x) = \boldsymbol x^\mathrm T S \boldsymbol x\) とできる. ◻

定義 1.10 (2変数関数の Hesse 行列, Hessian matrix)

2回偏微分可能な関数 \(f(x, y)\) に対し次の行列を Hesse 行列という

\[\begin{split}H (x, y) = \begin{bmatrix} \dfrac{\partial^2 f}{\partial x^2} & \dfrac{\partial^2 f }{\partial x \partial y} \\ \dfrac{\partial^2 f}{\partial y \partial x} & \dfrac{\partial^2 f}{\partial y^2} \end{bmatrix}\end{split}\]

備考 1.11

\(n\)変数関数の Hesse 行列は

\[\begin{split}H(x_1, \dotsc, x_n) = \begin{bmatrix} f_{x_1x_1} & \dots & f_{x_nx_1} \\ \vdots & \ddots & \vdots \\ f_{x_1x_n} & \dots & f_{x_nx_n} \end{bmatrix}.\end{split}\]

備考 1.12

英語で単に Hessian といえば, Hesse 行列の行列式になる. Hesse 行列は Hessian matrix という.

命題 1.13

関数 \(f(x, y)\) が2回連続微分可能な場合, Hesse 行列は対称行列になる.

Proof. 2回連続微分可能な関数では

\[\frac{\partial^2 f}{\partial y \partial x} = \frac{\partial^2 f}{\partial x \partial y}\]

が成立するので \(H(x, y)\) は対称行列となる. ◻

命題 1.13 は一般の\(n\)変数でも成立する. さて, 定理 1.5 (極小値をとるための条件) を Hesse 行列を用いて言い換えておこう.

定理 1.14

2回連続微分可能な関数 \(z=f(x, y)\) が \((x, y) = (a, b)\)で極小値をとるためには, 次の2つの条件が成立することが十分である.

条件 1（停留点）

\[\frac{\partial f}{\partial x}(a, b) = 0, \quad \frac{\partial f}{\partial y}(a, b) = 0\]

条件 2（正値性）

\((x, y)=(a, b)\) における Hesse 行列

\[\begin{split}H(a, b) = \begin{bmatrix} \dfrac{\partial^2 f}{\partial x^2}(a, b) & \dfrac{\partial^2 f}{\partial x \partial y}(a, b) \\ \dfrac{\partial^2 f}{\partial x \partial y}(a, b) & \dfrac{\partial^2 f}{\partial y^2}(a, b) \end{bmatrix}\end{split}\]

について, 任意の \(\boldsymbol x \in \mathbb R^2\), \(\boldsymbol x \ne 0\) に対し

\[Q_H(\boldsymbol x) := \boldsymbol x^{\mathrm T} H(a, b) \boldsymbol x > 0. \qquad \Box\]

対称行列と転置行列の性質

さて, \(f(x, y)\) が2回連続微分可能であれば, Hesse 行列は対称（\(\partial^2/\partial x \partial y = \partial^2/\partial y \partial x\)）だった.対称行列は以下に述べるような性質を持つ. 1年生の線形代数で学ぶ内容だが, 応用上きわめて重要なので, ぜひここで覚えてしまってほしい.

定理 1.15

実対称行列は必ず直交行列によって対角化できる. すなわち, 任意の実対称行列 \(S\) に対しある直交行列 \(U\) が存在し, 次のようにできる.

\[J = U^{-1} S U \quad J \text{ は対角行列} \qquad \Box\]

定理 1.16

実対称行列の固有値はすベて実数である.

定理 1.17

直交行列の逆行列はその転置行列に等しい.

\[U^{\mathrm T} = U^{-1} \qquad \Box\]

定理 1.15, 定理 1.16, 定理 1.17 から, 次が言える.

系 1.18

に対してある直交行列 \(U\) が存在し, 次のようにできる.

\[\begin{aligned} J = U^{\mathrm{T}}SU \quad J \text{ は対角行列}\end{aligned}\]

このとき, 対角行列 \(J\) の成分は全て実数となる.

備考 1.19

実対称行列はこのほかにも, 固有ベクトルが直交するなど, 応用上ありがたい性質をもつ. 詳しくは線形代数の教科書を見てほしい.

さて, 転置行列も応用でよく出てくる. 特に次の定理は重要である.

定理 1.20

(6)\[(AB)^\mathrm T = B^\mathrm T A^\mathrm T \label{eq: (AB)^T = B^T A^T} \qquad \Box\]

備考 1.21

定理 1.20 は, \(A\), \(B\) が正方行列でなくても成立する. 証明は線形代数の教科書に譲るとして, 行列とベクトルの大きさだけ確認しておこう. \(A\) が \(l \times m\) 行列, \(B\) が \(m \times n\) 行列のとき \(AB\) は \(l \times n\) 行列. \(B^\mathrm T\) は \(n \times m\) 行列, \(A^\mathrm T\) は \(m \times l\) 行列だから, \(B^\mathrm T A^\mathrm T=(AB)^\mathrm T\) は \(n \times l\) 行列.

\(n\)行の列ベクトルは \(n \times 1\) 行列とみなせるから, 式 (6) の特別な場合として, 行列とベクトルの積の転置について次が成立する.

系 1.22

行列 \(A\) とベクトル \(b\) の積の転置については次が成立する.

(7)\[(A\boldsymbol b)^\mathrm T = \boldsymbol b^\mathrm T A^\mathrm T \label{eq: (Ab)T = bTAT} \qquad \Box\]

例題 1.2

式 (7) を確かめよ.

\[\begin{split}A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}, \quad \boldsymbol b = \begin{bmatrix} x \\ y \end{bmatrix}\end{split}\]

解答例題 1.2 .

\[\begin{split}A \boldsymbol b = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix}x \\ y \end{bmatrix} =\begin{bmatrix} ax + by \\ cx + dy \end{bmatrix}\end{split}\]
\[(A \boldsymbol b)^\mathrm T = \left[ ax + by, \quad cx + dy \right]\]

一方

\[\begin{split}\begin{aligned} \boldsymbol b^\mathrm T A^\mathrm T & = \begin{bmatrix}x, \quad y \end{bmatrix}\begin{bmatrix} a & c \\ b & d \end{bmatrix} = \begin{bmatrix} xa + yb, \quad xc + yd \end{bmatrix} \\ & = \left[ ax + by, \quad cx + dy \right]\end{aligned}\end{split}\]

となり, \((A\boldsymbol b)^\mathrm T = \boldsymbol b^\mathrm T A^\mathrm T\) であることが分かる.

対称行列の対角化と2次形式の標準形

実対称行列は直交行列で対角化できる. これを用いて2次形式を標準形に変換することができる. この変形は, 極大・極小問題にとって極めて重要である.

例題 1.3

\(U\) により \(J = U^\mathrm T S U\) のように対角化できるとき, 2次形式

\[Q(\boldsymbol x) = \boldsymbol x^{\mathrm T} S\boldsymbol x\]

を対角化行列 \(J\) を用いて表せ.

解答例題 1.3 式 \(J = U^\mathrm T S U\) の両辺に左から \(U\), 右から \(U^{\mathrm T}\) を作用させると, \(U U^\mathrm T = U^\mathrm T U = E\)（\(E\) は単位行列）だから

\[U J U^{\mathrm T} = U \left(U^\mathrm T S U \right) U^{\mathrm T} = S\]

これを \(Q(\boldsymbol x) = \boldsymbol x^\mathrm T S \boldsymbol x\) に代入して

(8)\[Q(\boldsymbol x) = \boldsymbol x^\mathrm T U J U^\mathrm T \boldsymbol x \label{eq: Q = xT U J UTx}\]

解答はここまでとして, さらに変形を続ける. \(\boldsymbol{y} = U^{\mathrm{T}} \boldsymbol{x}\) とおくと 系 1.22 より

\[\boldsymbol y^\mathrm T = \left(U^\mathrm T \boldsymbol x\right)^\mathrm T = \boldsymbol x^\mathrm T U\]

これを用いて式 (8) を書き換えると, 次のようになる.

\[Q(\boldsymbol x) = \boldsymbol y^\mathrm T J \boldsymbol y\]

2変数の場合で考えよう.

\[\begin{split}\boldsymbol y = \begin{bmatrix} y_1 \\ y_2 \end{bmatrix}, \quad J= \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix}\end{split}\]

とおくと,

(9)\[\begin{split}\begin{aligned} Q(\boldsymbol x) & = \boldsymbol y^\mathrm T J \boldsymbol y = \begin{bmatrix} y_1 & y_2 \end{bmatrix} \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix} \begin{bmatrix} y_1 \\ y_2 \end{bmatrix} \notag \\ & = \lambda_1 y_1^2 + \lambda_2 y_2^2 \label{eq: quadratic form standard form}\end{aligned}\end{split}\]

式 (9) の形にした2次形式を（2次形式の）標準形 (canonical form) という. 標準形の \(y_1^2\), \(y_2^2\) の係数は, 2次形式の表現行列の固有値となる. この標準形から分かるように, \(\lambda_1 > 0\) かつ \(\lambda_2 > 0\) のとき, \(\boldsymbol y \ne \boldsymbol 0\) であれば \(Q(\boldsymbol x) > 0\) が成立する. さらに, \(U\) は直交行列なので \(\left\lVert \boldsymbol y \right\rVert = \left\lVert U^\mathrm T \boldsymbol x \right\rVert =\left\lVert \boldsymbol x \right\rVert\) だから [3], \(\boldsymbol y \ne \boldsymbol 0 \Leftrightarrow \boldsymbol x \ne \boldsymbol 0\) となり, 結局, 次の定理が成り立つことになる.

定理 1.23

実対称行列 \(S\) の固有値が全て正であれば, \(\boldsymbol x \ne \boldsymbol 0\) なる任意の \(\boldsymbol x\) に対して次が成立する.

(10)\[Q (\boldsymbol x) = \boldsymbol x^\mathrm T S \boldsymbol x > 0 \qquad \Box %\label{eq: positive quadratic form}\]

備考 1.24

定理 1.23 のように固有値が全て正の行列を正定値行列 (positive definite matrix) という. せっかくなので, 関連の用語をまとめておく.

定義 1.25 (正定値, 半正定値, 負定値, 半負定値)

  1. \(n \times n\) 実対称行列 \(A\) が正定値 (positive definite)であるとは, \(\boldsymbol x \ne \boldsymbol 0\) なる任意の \(n\) 次元ベクトル \(\boldsymbol x\) に対して　\(\boldsymbol x^{\mathrm T} A \boldsymbol x > 0\) が成立することである.

  2. \(n \times n\) 実対称行列 \(A\) が負定値 (negative definite)であるとは, \(\boldsymbol x \ne \boldsymbol 0\) なる任意の \(n\) 次元ベクトル \(\boldsymbol x\) に対して　\(\boldsymbol x^{\mathrm T} A \boldsymbol x < 0\) が成立することである.

  3. \(n \times n\) 実対称行列 \(A\) が半正定値 (positive semidefinite)あるいは非負定値 (nonnegative definite)であるとは, \(\boldsymbol x \ne \boldsymbol 0\) なる任意の \(n\) 次元ベクトル \(\boldsymbol x\) に対して　\(\boldsymbol x^{\mathrm T} A \boldsymbol x \ge 0\) が成立することである.

  4. \(n \times n\) 実対称行列 \(A\) が半負定値 (negative semidefinite)あるいは非正定値 (nonpositive definite)であるとは, \(\boldsymbol x \ne \boldsymbol 0\) なる任意の \(n\) 次元ベクトル \(\boldsymbol x\) に対して　\(\boldsymbol x^{\mathrm T} A \boldsymbol x \le 0\) が成立することである.

2変数関数の極大点・極小点のまとめ

以上の議論をまとめよう. 2変数関数 \(f(x, y)\) が2回連続微分可能であるとき, その Hesse 行列 \(H(x, y)\) は（すべての \((x, y)\) において）対称行列となる. さて, \((x, y) = (a, b)\) が2回連続微分可能な関数 \(f(x, y)\) の停留点であるとする. この時, \(H(a, b)\)（対称行列である）の固有値が全て正であれば, 定理 1.23 により, \(\boldsymbol{x} \ne \boldsymbol{0}\) なる \(\boldsymbol{x}\) について \(Q(\boldsymbol{x}) = {\boldsymbol{x}}^\mathrm T H(a, b) \boldsymbol{x} > 0\) が成立する, 従って \((a, b)\) は極小点となる. これを定理にまとめよう.

定理 1.26

2回連続微分可能な関数 \(z=f(x, y)\) が \((x, y) = (a, b)\)で極小値をとるためには, 次の2つの条件が成立することが十分である. 条件 1（停留点）

\[\frac{\partial f}{\partial x}(a, b) = 0, \quad \frac{\partial f}{\partial y}(a, b) = 0\]

条件 2（正値性） 点 \((a, b)\) における Hesse 行列の固有値が全て正である.

備考 1.27

極大点についても全く同様の議論ができる. \(z=f(x, y)\) が点 \((a, b)\) で極大値をとるためには, \((a, b)\) が停留点で, かつ, \((a, b)\) における Hesse 行列 \(H(a, b)\) の固有値が全て負であれば十分である. 停留点の Hesse 行列の固有値が正と負ならばその点は鞍点となる. また, もし Hesse 行列の固有値が0を含むならば, 極値の判定のためには, さらに高次の導関数を調べる必要がある.

3変数以上への拡張

前節までは, 基本的に2変数の場合のみを扱った. しかし, 第1.3.4節の対称行列と転置行列に関する部分は全ての次元の行列に対して言えるものであるし, Hesse 行列も2次形式も3変数以上の関数に対しても（備考に示したように）定義でき, 2次形式の標準化とその表現行列である対称行列の対角化が対応していることは3変数以上でも同じである. つまり, 3変数以上でも停留点における Hesse 行列の固有値を調べればその停留点が極大点か極小点か鞍点かいずれでもないか判定できるのである.

次に, この章の総まとめとして, \(n\)変数の場合の Hesse 行列と極大・極小についてまとめる.

定理 1.28

2回連続微分可能な実関数 \(z = f(\boldsymbol x)\), \(\boldsymbol x = \left[x_1, \dotsc, x_n\right]^\mathrm T\) の停留点　\(\boldsymbol a = \left[a_1, \dotsc, a_n\right]\)

\[\frac{\partial f}{\partial x_1}(\boldsymbol a) = \dotsb = \frac{\partial f}{\partial x_n}(\boldsymbol a) = 0\]

における Hesse 行列

\[\begin{split}H(\boldsymbol a) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1 \partial x_1} (\boldsymbol a) & \dots & \frac{\partial^2 f}{\partial x_1 \partial x_n} (\boldsymbol a) \\ \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} (\boldsymbol a) & \dots & \frac{\partial^2 f}{\partial x_n \partial x_n} (\boldsymbol a) \end{bmatrix}\end{split}\]

の固有値が (1) 全て正の実数であればこの停留点は極小値であり, (2) 全て負の実数であればこの点は極大値である. また, 固有値が (3) 正と負の数を含み 0 を含まない場合この停留点は鞍点であり, (4) 固有値が 0を含む場合, 極値判定のためには, さらに高次の微分係数を調べる必要がある.

Python による固有値の計算例

例 1.29

関数

\[z = f(x, y) = \cos (\pi x) \sin(\pi y)\]

に対して, \(\left[1, 1/2\right]^\mathrm T\) が 1) 停留点である（すなわち 1 階の導関数が 0 となる）ことを確認し, 2) この点における Hesse 行列の固有値からこの停留点が極大点か極小点かどちらでもないかを判定する.

{language=Python}
import numpy as np


def func(x):
    return np.cos(np.pi * x[0]) * np.sin(np.pi * x[1])


def grad(x):
    return np.array([
        - np.pi * np.sin(np.pi * x[0]) * np.sin(np.pi * x[1]),
        np.pi * np.cos(np.pi * x[0]) * np.cos(np.pi * x[1])
    ])


def hess(x):
    return np.array([
        [- np.pi  2 * np.cos(np.pi * x[0]) * np.sin(np.pi * x[1]),
          - np.pi  2 * np.sin(np.pi * x[0]) * np.cos(np.pi * x[1])],
        [- np.pi  2 * np.sin(np.pi * x[0]) * np.cos(np.pi * x[1]),
          - np.pi  2 * np.cos(np.pi * x[0]) * np.sin(np.pi * x[1])]
    ])


def main():
    x = np.array([1, 0.5])
    g = grad(x)
    h = hess(x)
    eigvals = np.linalg.eigvals(h)
    print("x = ", x)
    print("gradient of f at x = ")
    print(g)
    print("Eigenvalues of Hessian matrix at x = ")
    print(eigvals)


if __name__ == '__main__':
    main()

出力は以下のとおり.

x =  [1.  0.5]
gradient of f at x =
[-3.84734139e-16 -1.92367069e-16]
Eigenvalues of Hessian matrix at x =
[9.8696044 9.8696044]

1) \(\boldsymbol x =\left[ 1, 1/2\right]^\mathrm T\) における勾配（gradient）の値は

\[\begin{split}\nabla f (\boldsymbol x) = \begin{bmatrix} 0 \\ 0 \end{bmatrix},\end{split}\]

であるから, この点は停留点である. 2) \(\boldsymbol x =\left[ 1, 1/2\right]^\mathrm T\) における Hesse 行列の値は, ともに 9.869 で, 正である. よってこの点 \(\boldsymbol x =\left[ 1, 1/2\right]^\mathrm T\) は極小点である.

学習の参考に

線形代数を復習する場合, 応用上で出てきたトピックスに対して, 関連する部分を復習するのがよい. 大学1年生のときには, 線形代数を学ぶ意味など全く分からなかっただろうが, 応用上では, 行列式, 固有値・固有ベクトル, 2次形式, 線形空間と, 1年生で学ぶ線形代数の全ての分野が「役にたつ」ことが分かるだろう. 1年生で使った教科書が2 次形式までしっかりと解説してあればよいが, そうでない場合は, もう少し高度なテキストが必要であろう. 線形代数については, 優れた教科書は山ほどあるが, 筆者が使ったものの中で特に印象に残ったものとして, 以下を挙げておく.

  1. 児玉慎三, 須田信英, システム制御のためのマトリクス理論, コロナ社, 1978. https://www.coronasha.co.jp/np/isbn/9784339083309/

  2. 笠原皓司, 新装版改訂増補, 線形代数と固有値問題–スペクトル問題を中心に, 現代数学社, 2019. https://www.gensu.co.jp/book_print.cgi?isbn=978-4-7687-0519-3

洋書では,

  1. Strang, G, Introduction to linear algebra, 5th Ed., Cambridge University Press, 2016.

    邦訳も出ている. この本の著者のビデオ講義は世界的に人気である. 通読するのもよいと思う.

演習問題

次の関数 \(f(x)\) の (a) 1, 2, 3 階の導関数 \(f^\prime(x)\), \(f^{\prime\prime}(x)\), \(f^{(3)}(x)\) を求め, (b) それぞれの \(f(0)\), \(f^\prime(0)\), \(f^{\prime\prime}(0)\), \(f^{(3)}(0)\) の値を計算し, (c) 3 次の項までの Taylor 展開を求めよ. ただし, ここで \(\log\) は自然対数である.

例: \(f(x)=x^3\) の場合,

\[\begin{split}\begin{aligned} & (\mathrm a) \ f^\prime(x) = 3x^2, \quad f^{\prime\prime}(x) = 6x, \quad f^{(3)}(x) = 6 \\ & (\mathrm b) \ f(0)=0, \ \quad f^\prime(0) = 0, \quad f^{\prime\prime}(0) = 0, \quad f^{(3)}(0) = 6 \\ & (\mathrm c) \ f(x) = 0 + 0 x + \frac{1}{2!} x^2 + \frac{6}{3!} x^3 + R= x^3 + R\end{aligned}\end{split}\]

(1) \(f(x) = e^x\), (2) \(\log (1 + x)\), (3) \(\sin x\), (4) \(\cos x\) (5) \(\sinh x\), (6) \(\tan x\)

次の関数 \(f\) の2階導関数 (a) \(\partial^2 f/\partial x^2\), (b) \(\partial ^2 f/\partial x\partial y\), (c) \(\partial^2 f/\partial y^2\) を求めよ.

(1) \(f(x, y) = x^2 + y^2 + 2 x^2y^2\), (2) \(f(x, y) = x^2 + 2x + y^2 - 1\), (3) \(f(x, y) = \sin x \cos y\),

(4) \(f(x, y) = \sin (xy)\), (5) \(f(x, y) = \tan(x + y)\), (6) \(f(x, y) = e^{x + y}\)

(7) \(f(x, y) = e^{-\frac{x^2 + y^2}{2}}\), (8) \(f(x, y) = \log (xy), \quad (x>0, y>0)\)

(1) \(f(x) = \cos x \cos y\) の, \((x, y) = (0, 0)\) における次の導関数の値を求めよ.

(a) \(\frac{\partial f}{\partial x}(0, 0)\), (b) \(\frac{\partial f}{\partial y}(0, 0)\), (c) \(\frac{\partial^2 f}{\partial x^2}(0, 0)\), (d) \(\frac{\partial^2 f}{\partial x\partial y}(0, 0)\), (e) \(\frac{\partial^2 f}{\partial y^2}(0, 0)\)

(2) \(f(x) = e^{-\frac{x^2 + y^2}{2}}\) の, \((x, y) = (0, 0)\) における次の導関数の値を求めよ. (a) \(\frac{\partial f}{\partial x}(0, 0)\), (b) \(\frac{\partial f}{\partial y}(0, 0)\), (c) \(\frac{\partial^2 f}{\partial x^2}(0, 0)\), (d) \(\frac{\partial^2 f}{\partial x\partial y}(0, 0)\), (e) \(\frac{\partial^2 f}{\partial y^2}(0, 0)\)

\((x, y) = (0, 0)\) は (a) 次の関数の停留点であるか否か, (b) 停留点の場合, 極大点か極小点か鞍点かそれ以外かを答えよ.

(1) \(f(x, y) = x^2 + y^2 + 2 x^2y^2\), (2) \(f(x, y) = x^2 + 2x + y^2 - 1\)

  1. \(f(x, y) = \sin x \cos y\), (4) \(f(x, y) = \sin (xy)\)

  1. \(f(x, y) = \tan(x + y)\), (6) \(f(x, y) = e^{x + y}\)

(7) \(f(x, y) = e^{-\frac{x^2 + y^2}{2}}\), (8) \(f(x, y) = \log (xy), \quad (x>0, y>0)\)

次の各行列に対して二次形式 \(Q(\boldsymbol x)\) を求めよ. ただし \(\boldsymbol x=\begin{bmatrix} x & y \end{bmatrix}\) とする.

\[\begin{split}(1) \ A = \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}, \quad (2) \ B = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}, \quad (3) \ C = \begin{bmatrix} \pi/2 & -\pi/2 \\ \pi/2 & \pi/2 \end{bmatrix}, \quad (4) \ D = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\end{split}\]

次のようなベクトルと行列を考える.

\[\begin{split}\boldsymbol a = \begin{bmatrix} a \\ b \end{bmatrix}, \quad A = \begin{bmatrix} a & b \\ c & d \\ e & f \end{bmatrix}, \quad G = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}\end{split}\]

これらのベクトル, 行列について次の計算をせよ. (1) \(\boldsymbol a^{\mathrm T} \boldsymbol a\), (2) \(\boldsymbol a \boldsymbol a^{\mathrm T}\), (3) \(AG\), (4) \(GA\), (5) \(AA^{\mathrm T}\).

次の行列の (1) 固有値を求め, (2) 正定値行列か, 負定値行列か, どちらでもないか答えよ.

\[\begin{split}\begin{aligned} A = \begin{bmatrix} 3 & 1 \\ 1 & 3 \end{bmatrix}, \quad B = \begin{bmatrix} 3 & -1 \\ -1 & 3 \end{bmatrix}, \quad C = \begin{bmatrix} -3 & 1 \\ 1 & -3 \end{bmatrix}, \quad D = \begin{bmatrix} 1 & 3 \\ 3 & 1 \end{bmatrix}\end{aligned}\end{split}\]

次の対称行列が正定値か負定値か, どちらでもないか示せ.

\[\begin{split}A = \begin{bmatrix} 5 & 2 \\ 2 & 5 \end{bmatrix}, \quad B = \begin{bmatrix} 4 & 1 \\ 1 & - 2 \end{bmatrix}, \quad C = \begin{bmatrix} 1 & 3 \\ 3 & -3 \end{bmatrix}, \quad D = \begin{bmatrix} -2 & -1 \\ -1 & 2 \end{bmatrix}\end{split}\]

(1) 次の関数について, \((x, y)=(1, 1)\) が停留点であることを確かめ, (2)　これが極小点か極大点か鞍点かいずれでもないか答えよ.

\[f(x, y) = \log(x y) - \frac{1}{3} \left( x^3 + y^3 \right)\]

(1) 次の関数について, \((x, y, z)=(0, 0, 0)\) が停留点であることを確かめよ. (2) また, \((x, y, z)=(0, 0, 0)\) が極小点か極大点か鞍点かいずれでもないか答えよ.

固有値の計算には Python の Numpy, Wolfram Alpha のツールを用いよ.

\[f(x, y, z) = 2x^2 + 2y^2 + 2z^2 - xy - yz - zx\]

次の関数の (1) 停留点を求め, (2) その停留点が極小点か極大点か鞍点かいずれでもないか答えよ.

\[f(x, y) = (x + y- 3)^2 + 2 (x-1)^2 + (y-1)^2\]

◀ Previous TOC Next ▶