TOC

3. 母集団と標本・記述統計量

3.1 統計量（statistic）とは

母集団と標本

母集団（population）の性質（母数, parameter）を知るために, ある大きさ（size）の標本（sample）をとり, 標本の性質を調べる.
標本の性質から母集団の性質を推定（infer）する.

母数（parameter）と統計量（statistic）

母集団（population）の性質を表す定数を母数（parameter）という.
- 分布の期待値や分散は, 母数である.
母集団の性質（母数）を知るために, ある大きさ（size）の標本（sample）をとり, 標本の性質を調べる.
データ（標本）の関数として得られる数を統計量（statistic）という.
位置母数（location parameter）
- 例: 期待値 \(\mu\)
尺度母数（scale paramer）
- 例: （正規分布の）標準偏差 \(\sigma\)
形状母数（shape parameter）
- 例: パレート分布の指数

標本（無作為標本, random sample）

母集団からの無作為抽出による標本
同じ母集団からとり, 相互に独立な確率変数である.
このような性質をもつ確率変数を独立同分布（independent and identically distributied, よく iid と略される）の確率変数
母集団の分布が（未知の場合を含み）仮定できる場合, 次のような言い方をする.
- \(F_X\) に従う母集団からの大きさ \(n\) の無作為標本
- あるいは, \(F_X\) 従う \(n\) 個の独立同分布（iid）確率変数

標本の大きさ（サイズ）と標本数

世論調査で 500 人を無差別抽出してアンケートをとったとき, 標本の大きさ（sample size）が 500 である.
シミュレーションで, 大きさ 20 のサンプルを生成し, その統計量を計算する. このとき, 大きさ 20 のサンプルを繰り返して 10 回作成し, 解析した場合, 標本数（the number of samples）が 10 である.

3.2 中心傾向

平均（mean）

母集団の平均

\[\mu = \mathbb E (X) = \int x \, dF(x) \tag{2.9}\]

定義 3.1（標本平均, sample mean）

この母集団から, 大きさ \(n\) の標本をとると考える. 標本を \(\{X_i\}\) \((i = 1, \dotsc, n)\) と表す.

\[\bar X = \frac{\sum_{i=1}^n X_i}{n} \tag{3.1}\]

Remark

\(\mu\) はパラメーター, \(\bar X\) は統計量である.
\(\bar X\) は標本の算術平均

定理 3.1

母平均を \(\mu\), 無作為標本の標本平均を \(\bar X\) とするとき, 次が成り立つ.

\[\mathbb E ( \bar X ) = \mu \tag{3.2}\]

証明

\(\mathbb E\) の演算が積分（線形）であることから

\begin{align*} \mathbb E \bar X & = \mathbb E \left(\frac{1}{n} \sum_{i=1}^n X_i\right) = \frac{1}{n} \mathbb E \left( \sum_{i=1}^n X_i \right) \\ & = \frac{1}{n} n \, \mathbb E (X_i) = \mu \end{align*}

Remark

標本の平均 \(\bar X\) は確率変数である. その期待値は母平均 \(\mu\) である.
統計学では, \(\mathbb E(X_i)\) の代わりに \(\mathbb E(X_1)\) と書く慣習もある.

定義 3.2（中央値, median）

データを順番にならべたときに, ちょうど真ん中に位置する値
データが偶数の場合, 中央に位置する 2 つの値の算術平均をとる.

\[\operatorname{median} = \frac{1}{2} \left( X_{\left(\frac{n}{2} \right)} + X_{\left(\frac{n}{2} + 1\right)} \right) \tag{3.3}\]

ここで \(X_{(i)}\) は標本の順序統計量で, すべての観測値を (重複も含め) 小さいものから順番に並べたときに \(i\) 番目の値である.

例題 3.1

ある母集団から標本をとって, 次のような値が得られた.

\[\boldsymbol x = [ 1, 3, 9, 24, 36, 42 ]\]

この標本平均と中央値を求めよ.

解答例 3.1

\[\bar X = \frac{1 + 3 + 9 + 24 + 36 + 42}{6} = 19.17\]

\[\operatorname{median} = \frac{9 + 24}{2} = 16.5\]

3.3 ばらつき（Variability）

範囲（range）

数値の集合の範囲（range）とは, その集合の最大値と最小値の差である.
母集団の範囲
- 無限大になり得る.
標本の範囲

\[\operatorname{Range} = \max(\{X_i\}) - \min(\{X_i\}) \quad (i = 1, \dotsc, n) \tag{3.4}\]

四分位数, 四分位範囲

データを小さいものから並べたとき, 25%. 50%, 75% の値を四分位数という.
25% のものを第一四分位数, 50% のものを第二四分位数（メディアンと同じ）, 75% のものを第三四分位数という.

分散（variance）

母集団の分散

\[\sigma^2 := \mathbb E(X - \mu)^2 \tag{2.10}\]

定義 3.3（標本分散, sample variance）

ある母集団からの大きさ \(n\) の標本の標本分散 \(S^2\) は

\begin{equation} S^2 := \frac{1}{n-1} \sum_{i = 1}^n (X_i - \bar X)^2 \tag{3.5} \label{eq: sample variance} \end{equation}

Remark

なぜ \(n\) ではなく \(n-1\) で割るのかについては後述.
標本分散 \(S^2\) は確率変数である.

定理 3.2

母分散を \(\sigma^2\) 無作為標本の標本分散を \(S^2\) とするとき, つぎが成り立つ.

\[\mathbb E S^2 = \sigma^2 \tag{3.6}\]

定義 3.4 （標準偏差, standard deviation）

母集団の標準偏差

\[\sigma = \sqrt{\sigma^2} \tag{3.7}\]

標本標準偏差

\[S = \sqrt{S^2} \tag{3.8}\]

例題 3.2

例題 3.2 の標本

\[\boldsymbol x = [ 1, 3, 9, 24, 36, 42 ]\]

この標本の標本分散を求めよ.

解答例 3.2

\begin{align*} s^2 = \frac{1}{6 - 1} & \bigg[ (1 - \bar X)^2 + (3 - \bar X)^2 + (9 - \bar X)^2 \\ & + (24 - \bar X)^2 + (36 - \bar X)^2 + (42 - \bar X)^2 \bigg] \\ & = 304.56666666 \approx 304.6 \end{align*}

例題 3.3

Pandas, または R を使って, 次のデータの平均, 標準偏差, 最小値, 四分位数, 最大値を求めよ.

:nbsphinx-math:`begin{align*} boldsymbol x = [& 73, 18, 45, 28, 27, 52, 41, 41, 90, 18,

\ & 16, 63, 74, 19, 40, 38, 97, 54, 63, 71, \ & 69, 79, 61, 27, 12, 48, 35, 99, 8, 29, \ & 40, 72, 57, 10, 63, 95, 97, 10, 23, 18, \ & 75, 58, 82, 58, 44, 71, 5, 59, 55, 52]

end{align*}`

[1]:

#### 3.3
import pandas as pd

x =[73,18,45,28,27,52,41,41,90,18,
    16,63,74,19,40,38,97,54,63,71,
    69,79,61,27,12,48,35,99,8,29,
    40,72,57,10,63,95,97,10,23,18,
    75,58,82,58,44,71,5,59,55,52]
df = pd.DataFrame()
df['x'] = x
df.describe()

[1]:

	x
count	50.000000
mean	49.580000
std	26.272582
min	5.000000
25%	27.250000
50%	52.000000
75%	70.500000
max	99.000000

解答例 3.3

\[\bar X = 49.58, \ S = 26.27, \ X_\mathrm{min} = 5, \ X_{0.25} = 27.25\]

\[X_{0.75} = 70.5, \ X_\mathrm{max} = 99\]

3.4 大数の法則

大数の法則（Law of Large Numbers）

定理 3.1（大数の弱法則, weak law of large numbers）

\(X_1, X_2, \dotsc\) を, 平均 \(\mu\), 分散 \(\sigma^2 < \infty\) の母集団からの, 独立同分布に従う（independent and identically distributed）確率変数とする.
\(X_1, X_2, \dotsc\) の, 第 \(n\) 項までの平均を \(\bar X_n\) と定義する.

\[\bar X_n := \frac{1}{n} \sum_{i=1}^n X_i \tag{3.9}\]

このとき, 任意の \(\varepsilon >0\) に対して

\[\lim_{n\to \infty}\mathbb P(\lvert \bar X_n - \mu \rvert < \varepsilon) = 1 \tag{3.10}\]

Remark

次のように表現されることもある.

\[\lim_{n\to \infty}\mathbb P(\lvert \bar X_n - \mu \rvert \ge \varepsilon) = 0\]

大数の法則が言っているのは, 標本を大きくすれば標本平均は限りなく母平均に近づくということである.
式 (3.10) を理解できなくても, （確率的に）\(n \to \infty\) で標本平均 \(\to\) 母平均, が理解できればよい.
大数の弱法則と別に, 大数の強法則（strong law of large numbers）もある. この区別については, 測度論などが必要になるので, ここでは触れない. 応用上は弱法則で十分である.

3.5 中心極限定理（Central Limit Theorem）

中心極限定理（Central Limit Theorem）

大数の法則は, 標本平均の値についての定理である.
中心極限定理は, 標本平均の分布に関する定理である.

正規分布

平均 \(\mu\), 分散 \(\sigma^2\) の正規分布（このノートでは, \(\mathcal N(\mu, \sigma^2)\) で表す）の確率密度関数と累積分布関数は以下で与えられる.
これらの式を覚える必要はない. 必要に応じて web 等を参照すれば良い.
連続分布である.

\[f_X(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi} \sigma} e^{-(x - \mu)^2 / (2 \sigma^2)} \tag{3.11}\]

\begin{align*} F_X(x; \mu, \sigma) & = \mathbb P \left( \frac{X - \mu}{\sigma} \le x \right) \\ & = \frac{1}{\sqrt{2 \pi}}\int_{-\infty}^x e^{-t^2 / 2} \, dt, \quad t = \frac{x - \mu}{\sigma} \tag{3.12} \end{align*}

定理 3.2（中心極限定理, central limit theorem）

\(X_1, X_2, \dotsc\) を, 平均 \(\mu\), 分散 \(\sigma^2 < \infty\) の母集団からの, 独立同分布に従う（independent and identically distributed）確率変数とする.
\(X_1, X_2, \dotsc\) の, 第 \(n\) 項までの平均を \(\bar X_n\) とする.
このとき,

\[\lim_{n\to\infty} \frac{\sqrt{n} (\bar X_n - \mu)}{\sigma} \sim \mathcal N(0, 1) \tag{3.13}\]

あるいは \(n\) が大きいときに近似的に, 次が成立する.

\[\bar X_n \approx \mathcal N \left(\mu, \frac{\sigma^2}{n} \right) \tag{3.14}\]

中心極限定理が言っているのは, サンプル数が増えると, 標本平均の分布が, 平均 \(\mu\), 分散 \(\sigma^2/n\) の正規分布に近づく, ということである.
式 (3.13) は, 左辺のみに \(n\) が含まれている.
式 (3.13) は, 右辺に \(n\) がふくまれているので, 極限の形にはならない. これは近似式である.
中心極限定理の証明は, この講義の範囲外ということで, 省略する. 興味のある人は, 確率の教科書, web 上の情報などを参照されたし.
\(X_1, X_n, \dotsc,\) の条件, 分散 \(\sigma^2 < \infty\) は必須である. これが成立しない場合に, さらに別の条件下で和は安定分布に収束する. 安定分布はこの講義の範囲外である.

例題 3.4

Python の scipy.stats などを使って, 指数分布の rate parameter \(\lambda = 2\) のときの, 平均値の分布求める.
サンプルの大きさ（サンプルサイズ）\(n = 3, 10, 30\) の場合について, 平均値を求め, それを 10000 回繰り返して, 平均値のヒストグラムを示せ.
ヒストグラムに, 中心極限定理から計算される正規分布の密度関数をプロットせよ（指数分布の平均と分散については, web 上で検索せよ）.

[3]:

import matplotlib.pyplot as plt
import pandas as pd
import scipy.stats


fig, ax = plt.subplots(figsize=(4, 3))
x = scipy.stats.expon.rvs(1, size=10000)
ser = pd.Series(x)
ser.hist(ax=ax, bins=40, alpha=.5)
print('参考: 指数関数のヒストグラムの例')

参考: 指数関数のヒストグラムの例

../_images/basic_statistics_2022_Lecture_030_26_1.png

解答例

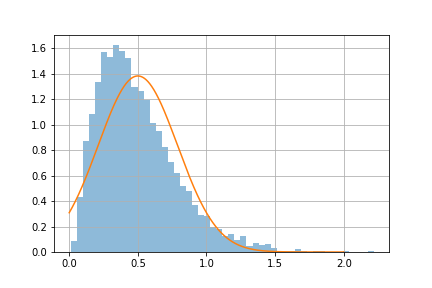
Exponential sim size 3

\(\textsf{指数分布}\), Rate parameter \(\lambda_0 = 2 \textsf{ からのサンプルサイズ } n=3\textsf{ の標本平均の分布}\)

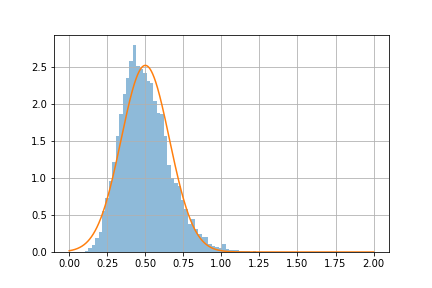
Exponential sim size 10

\(\textsf{指数分布}\), Rate parameter \(\lambda_0 = 2 \textsf{ からのサンプルサイズ } n=10 \textsf{ の標本平均の分布}\)

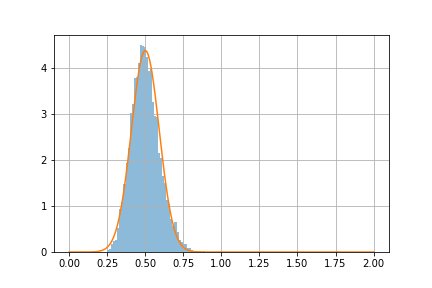
Exponential sim size 30

\(\textsf{指数分布}\), Rate parameter \(\lambda_0 = 2 \textsf{ からのサンプルサイズ } n=30 \textsf{ の標本平均の分布}\)

Remark

指数関数の場合, サンプルサイズが小さいと, 標本平均の分布は正規分布にはならない（今週の宿題の, 正規分布の場合と比較せよ）.
検定における, 正規分布の仮定（次回の講義）が重要であることが分かる.

3.6 標本分散について

標本分散はなぜ \(n-1\) で割るのか 1

母分散の定義 \(\sigma^2 = \mathbb E (X - \mu)^2\), と標本分散の定義 \(\frac{1}{n-1} \sum (X_i - \bar X)\)
母分散の定義では \(\mu\) を, 標本分散では, \(\bar X\) を引いている.
ここに鍵がある.
まず, 次の補題を用意する.

補題 3.1

\[\sum_{i=1}^n (x_i - a)^2 = \sum_{i=1}^n (x_i - \bar x)^2 + n(\bar x - a)^2 \tag{3.15}\]

ただし, \(a\) は定数で

\[\bar x = \frac{1}{n}\sum_{i=1}^n x_i\]

補題 3.1 の証明

\begin{align*} \sum_{i=1}^n (x_i - a)^2 &= \sum_{i=1}^n (x_i - \bar x + \bar x - a)^2 \\ & = \sum_{i=1}^n (x_i - \bar x)^2 + 2 \sum_{i=1}^n (x_i - \bar x) (\bar x - a) + \sum_{i=1}^n (\bar x - a)^2 \end{align*}

ところが,

\[\sum_{i=1}^n (x_i - \bar x) (\bar x - a) = (\bar x - a) \sum_{i=1}^n (x_i - \bar x) = 0\]

\[\sum_{i=1}^n (\bar x - a)^2 = n (\bar x - a)^2\]

したがって,

\begin{align*} \sum_{i=1}^n (x_i - a)^2 = \sum_{i=1}^n (x_i - \bar x)^2 + n (\bar x - a)^2 \end{align*}

標本分散はなぜ \(n-1\) で割るのか 2*

定理 3.2 \(\mathbb E S^2 = \sigma^2\) の証明.
補題 3.1 より

\begin{align*} \sum_{i = 1}^n (X_i - \mu)^2 = \sum_{i = 1}^n (X_i - \bar X)^2 + n (\bar X - \mu)^2 \end{align*}

両辺の期待値をとっても, 等号はなりたつ

\begin{align*} \underbrace{\mathbb E \left[\sum_{i = 1}^n (X_i - \mu)^2 \right]}_{= n \sigma^2}= \mathbb E \left[\sum_{i = 1}^n (X_i - \bar X)^2 \right] + \underbrace{\mathbb E \left[ n (\bar X - \mu)^2 \right]}_\mathrm{(b)} \tag{3.16} \end{align*}

1. は

\begin{align*} \mathbb E (\bar X - \mu)^2 &= \mathbb E\left(\frac{\sum_{i=1}^n X_i}{n} - \mu \right)^2 %\\& = \mathbb E \left\{\frac{\sum_{i=1}^n \left(X_i - \mu\right)}{n}\right\}^2 \\ & = \frac{1}{n^2}\underbrace{\mathbb E \sum_{i=1}^n (X_i - \mu)^2}_{n \sigma^2}+ \frac{1}{n^2}\underbrace{\mathbb E \left[\sum_{i=1}^n \sum_{j \ne i} (X_i - \mu)(X_j - \mu) \right]}_{=0, \ X_i, X_j \textsf{は独立}} \end{align*}

よって, 式 (3.16) は

\[n\sigma^2 = \mathbb E \left[\sum_{i = 1}^n (X_i - \bar X)^2 \right] + \sigma^2\]

\[\therefore \quad \mathbb E S^2 = \mathbb E \left[ \frac{1}{n-1} \sum_{i = 1}^n (X_i - \bar X)^2 \right] = \frac{1}{n-1} \mathbb E \left[\sum_{i = 1}^n (X_i - \bar X)^2 \right] = \sigma^2\]

標本分散の定義について

標本分散の定義として

\[S^2 = \frac{1}{n} \sum_{i=1}^n (X_i - \bar X)^2 \tag{3.17} \label{eq: biased sample variance}\]

が使われることもある.

式 \eqref{eq: biased sample variance} の \(S^2\) を標本分散, 式 (3.5) の \(S^2\) を（標本）不偏分散と呼んで区別することもある.
英語では, 共に標本分散（sample variance）で, その文献における定義に注意するしかない.
本テキストでは, 定義 3.3 （式 3.4）を用い, 用語として「標本分散」を用いる. これは英語では不偏分散という用語は一般的でないことを考慮したものである.
とはいえ, 混乱は避けたいので, 前後から定義が明らかな場合以外は, 「標本分散（不偏分散）」という記述を心がける. 少々煩雑になるが, 現状を考えると, これが妥協点かと考える.

◀ Previous

TOC

Next ▶

基礎統計学

3. 母集団と標本・記述統計量

3.1 統計量（statistic）とは

母集団と標本

母数（parameter）と統計量（statistic）

標本（無作為標本, random sample）

標本の大きさ（サイズ）と標本数

3.2 中心傾向

平均（mean）

定義 3.1（標本平均, sample mean）

Remark

定理 3.1

証明

Remark

定義 3.2（中央値, median）

例題 3.1

解答例 3.1

3.3 ばらつき（Variability）

範囲（range）

四分位数, 四分位範囲

分散（variance）

定義 3.3（標本分散, sample variance）

Remark

定理 3.2

定義 3.4 （標準偏差, standard deviation）

例題 3.2

解答例 3.2

例題 3.3

解答例 3.3

3.4 大数の法則

大数の法則（Law of Large Numbers）

定理 3.1（大数の弱法則, weak law of large numbers）

Remark

3.5 中心極限定理（Central Limit Theorem）

中心極限定理（Central Limit Theorem）

正規分布

定理 3.2（中心極限定理, central limit theorem）

例題 3.4

解答例

Remark

3.6 標本分散について

標本分散はなぜ \(n-1\) で割るのか 1

補題 3.1

補題 3.1 の証明

標本分散はなぜ \(n-1\) で割るのか 2*

標本分散の定義について