TOC

3. シミュレーション・大数の法則・中心極限定理

3.1 大数の法則

想定する場面

繰り返し実験（同じ条件で実験を繰り返して複数のデータを得, その平均値をとる）
次のいずれかの条件が成り立つ場合を想定.
- 有限の母集団から, 復元抽出を行う.
- 母集団が十分大きく, サンプリングが母集団の分布に影響を及ぼさないと考えられる.
サンプルされる量はランダムなので, これを確率変数 \(X\) で表す.
サンプルサイズが 1 から大きくなっていく状況を, 得られたデータ列として, 次で表す.

\[X_1, X_2, \dotsc\]

繰り返し実験の場合は, 1 回目の結果が \(X_1\), 2 回目の結果が \(X_2\), ということになる.
サンプルサイズ \(n\) のときは, サンプル（標本）は

\[\boldsymbol X = [X_1, X_2, \dotsc, X_n]\]

サンプルサイズ \(n\) の時の標本平均を \(\bar X_n\) と表す.

\[\bar X_n = \frac{X_1 + \dotsc + X_n}{n}\]
大数の法則は, サンプルサイズが大きくなると, 標本平均は母集団の平均 \(\mu\) に近づくことを主張する.

定理 3.1（大数の弱法則, weak law of large numbers）

\(X_1, X_2, \dotsc\) を, 平均 \(\mu\), 分散 \(\sigma^2 < \infty\) の母集団からの, 独立同分布に従う（independent and identically distributed, iid）確率変数とする.
\(X_1, X_2, \dotsc\) の, 第 \(n\) 項までの平均を \(\bar X_n\) と定義する.

\[\bar X_n := \frac{1}{n} \sum_{i=1}^n X_i \tag{3.1}\]

このとき, 任意の \(\varepsilon >0\) に対して

\[\lim_{n\to \infty}\mathbb P(\lvert \bar X_n - \mu \rvert < \varepsilon) = 1 \tag{3.2}\]

大数の法則が言っていること

標本平均は, 標本サイズが大きくなればなるほど, 母集団の平均 \(\mu\) に近づく.

\(X_1, X_2, \dotsc\) は \(\{X_k\}\), \(\{X_k\}_1^\infty\) などと書かれることもある.

3.2 中心極限定理

定理 3.2（中心極限定理, central limit theorem）

\(X_1, X_2, \dotsc\) を, 平均 \(\mu\), 分散 \(\sigma^2 < \infty\) の母集団からの, 独立同分布に従う（independent and identically distributed, iid）確率変数とする.
\(X_1, X_2, \dotsc\) の, 第 \(n\) 項までの平均を \(\bar X_n\) とする.
このとき,

\[\lim_{n\to\infty} \frac{\sqrt{n} (\bar X_n - \mu)}{\sigma} \sim \mathcal N(0, 1) \tag{3.3}\]

あるいは \(n\) が大きいときに近似的に, 次が成立する.

\[\bar X_n \sim \mathcal N \left(\mu, \frac{\sigma^2}{n} \right) \tag{3.4}\]

ここで, \(\sim\) は, 左辺が右辺の分布に従う（あるいは右辺が左辺の分布に従う）ことを示す.

3.3 シミュレーション

確率変数の発生

scipy.stats.norm.rvs(loc=0, scale=1, size = n)

例題 3.1

平均 \(\mu=0\), 分散 \(\sigma^2 = 1\) の正規分布（\(\mathcal N(0, 1)\)）に従う確率変数を 10 個生成して小さい順に並べよ.

[1]:

# 3.1
import numpy as np
import scipy.stats

n = 10
xs = scipy.stats.norm.rvs(size=n)
xs.sort()
print(xs)
# print(repr(xs))

[-1.36429552 -0.77566098 -0.61215486 -0.43896242 -0.37173139 -0.09419727
  0.0064787   0.13017226  0.87103925  0.95399621]

例題 3.2

平均 \(\mu = 10\), 分散 \(\sigma^2 = 2\) の正規分布（\(\mathcal N(10, 2)\)）に従う確率変数を 10 個生成して小さい順に並べよ.

[2]:

# 3.2
import scipy.stats

n = 10
xs = scipy.stats.norm.rvs(loc=10, scale=2**0.5, size=n)
xs.sort()
print(repr(xs))

array([ 7.64824291,  9.40805099,  9.73024785, 10.39558245, 10.62611729,
       10.68488512, 10.72499778, 10.85591543, 10.93656338, 11.43156841])

例題 3.3

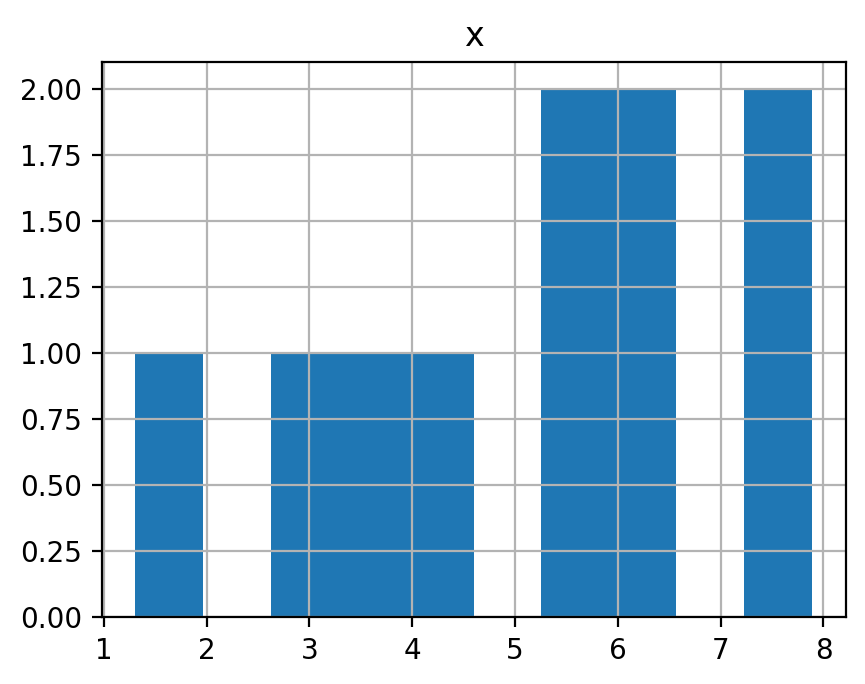
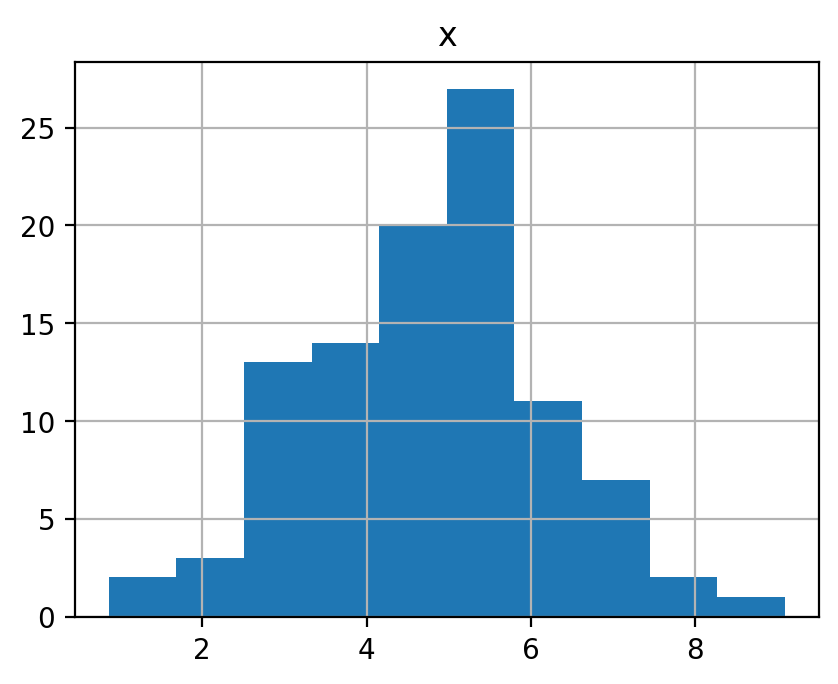
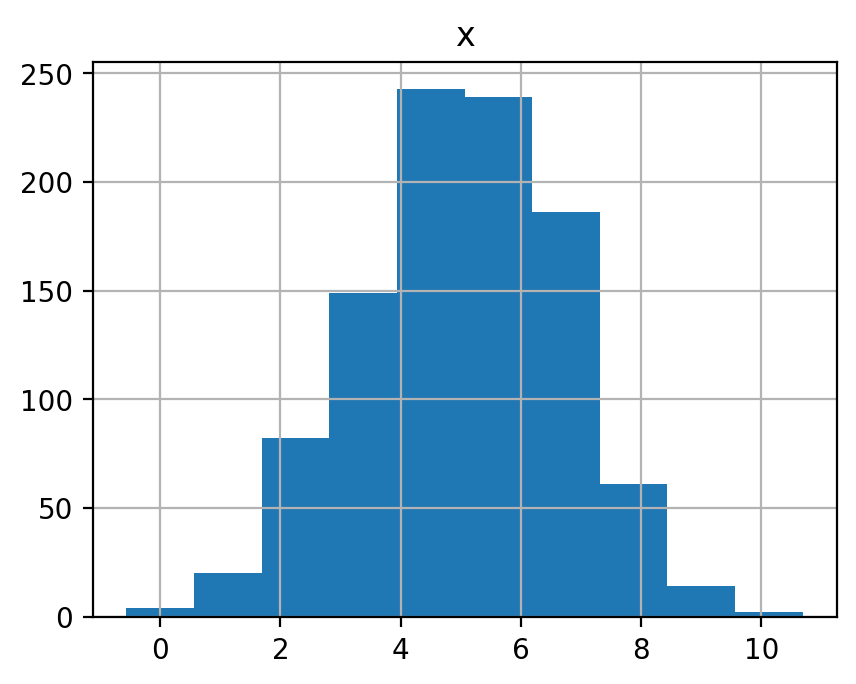
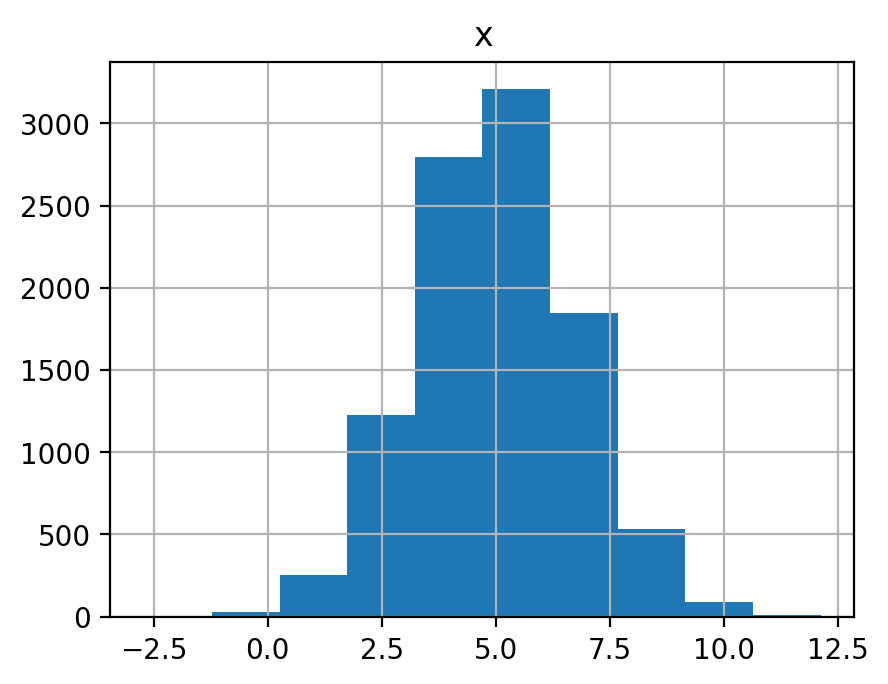
平均 \(\mu=5\), 分散 \(\sigma^2=3\) の正規分布（\(\mathcal N(5, 3)\)）に従う確率変数を 10, 100, 1000, 10000 個生成してそれぞれヒストグラムを表示せよ. また, それぞれの平均を示せ.

[1]:

import scipy.stats
import pandas as pd


ns = [10, 100, 1000, 10000]
for n in ns:
    xs = scipy.stats.norm.rvs(loc=5, scale=3**0.5, size=n)
    df = pd.DataFrame()
    df['x'] = xs
    df.hist()
    print(df['x'].mean())

5.180606363456557
4.7590275362682535
5.021853683012705
5.016899857129533

../_images/exercise_measurement_2021_Lecture_030_14_1.png

../_images/exercise_measurement_2021_Lecture_030_14_2.png

../_images/exercise_measurement_2021_Lecture_030_14_3.png

../_images/exercise_measurement_2021_Lecture_030_14_4.png

3.4 中心極限定理のシミュレーション

例題 3.4

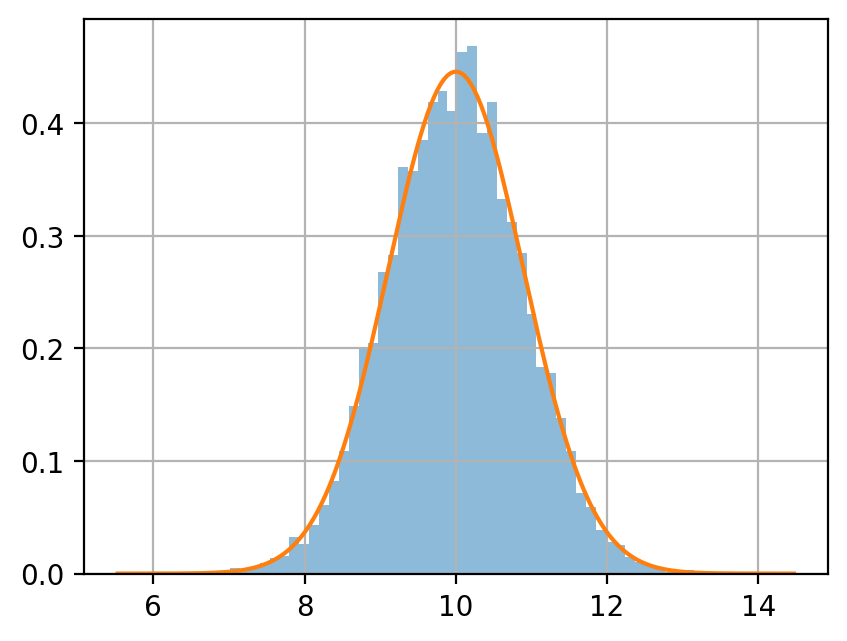
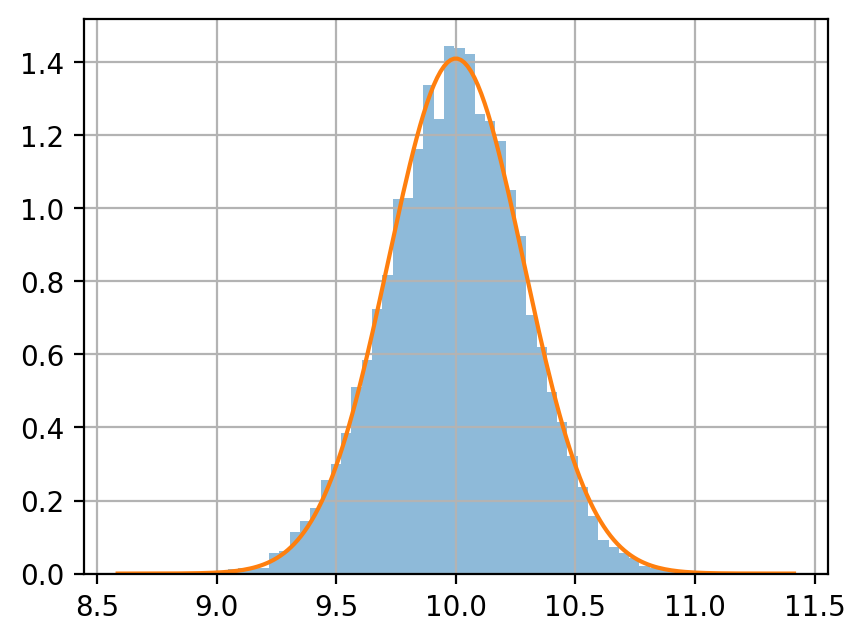
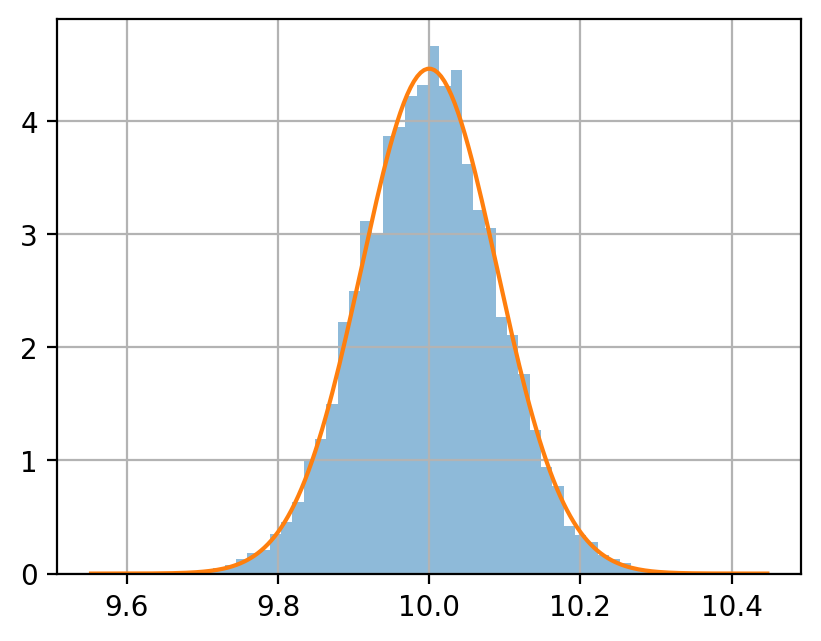
正規分布 \(\mathcal N(10, 4)\) に従う確率変数を生成する.
サンプルサイズ \(n = 5, 50, 500\) のサンプルを, それぞれ 10000 個生成し, 各サンプルサイズにおける平均値をヒストグラムに示せ.
同じグラフに, \(\mathcal N(10, 4/n)\) の密度関数をプロットせよ.
ヒストグラムと密度関数を比較するときは, pandas.DataFrame.hist(density=True) を指定する.

[3]:

import matplotlib.pyplot as plt
import numpy as np
import scipy.stats


df = pd.DataFrame()
ns = [5, 50, 500]
n_rep = 10000
for i, n in enumerate(ns):
    fig, ax = plt.subplots()
    ms = []
    for i_rep in range(n_rep):
        xs = scipy.stats.norm.rvs(loc=10, scale=4**.5, size=n)
        ms.append(xs.mean())
    ssize = str(n)
    df[ssize] = ms

    df[ssize].hist(density=True, bins=50, ax=ax, alpha=.5)

    xps = np.linspace(10 - 10/n**.5, 10 + 10/n**.5, 200, 100)
    fs = scipy.stats.norm.pdf(xps, loc=10, scale=(4/n)**.5)
    ax.plot(xps, fs)

df.describe()

[3]:

	5	50	500
count	10000.000000	10000.000000	10000.000000
mean	9.994740	9.993461	9.999267
std	0.887653	0.283335	0.089576
min	6.623542	8.961125	9.639867
25%	9.381909	9.804096	9.939069
50%	10.007930	9.998335	9.999874
75%	10.590642	10.187395	10.058958
max	13.155734	11.112053	10.387042

../_images/exercise_measurement_2021_Lecture_030_17_1.png

../_images/exercise_measurement_2021_Lecture_030_17_2.png

../_images/exercise_measurement_2021_Lecture_030_17_3.png

例題 3.5

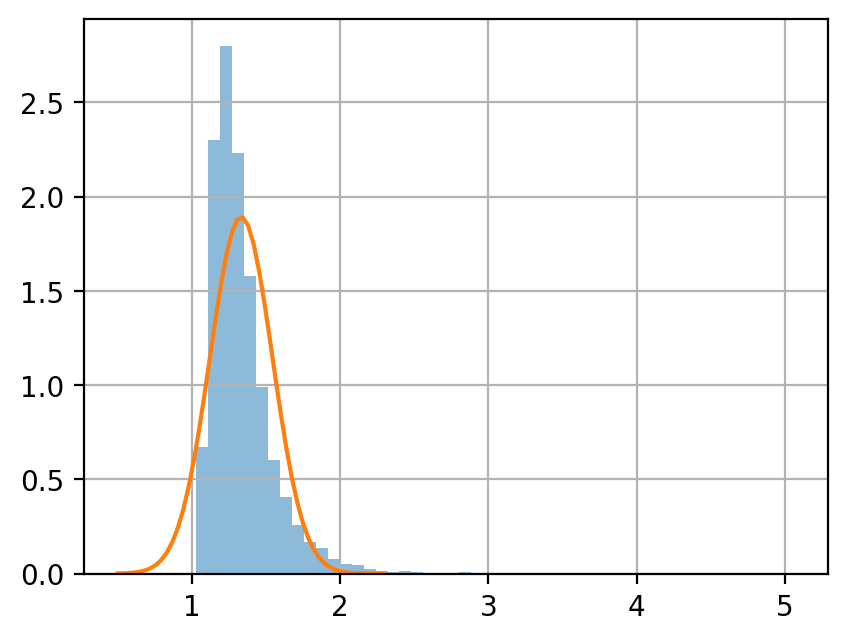
母数 \(\eta = 1\), \(\alpha = 4\) のパレート分布を考える.

\[F(x; \eta, \alpha) = 1 - \eta / x^\alpha\]

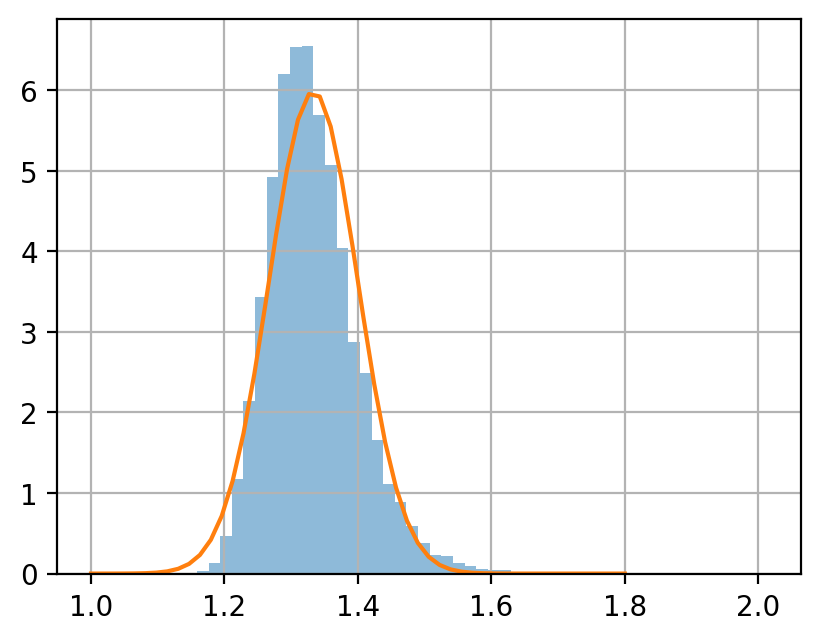
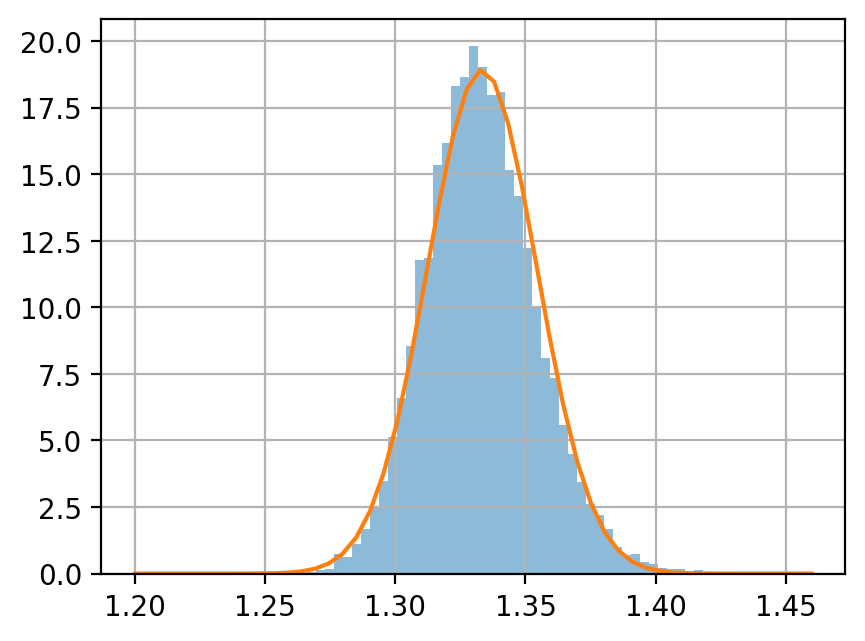
サンプルサイズ \(n = 5, 50, 500\) のサンプルを, それぞれ 10000 個生成し, 各サンプルの平均値をヒストグラムに示せ.
中心極限定理によると, サイズ \(n\) 平均値の分布は次に従う.

\[\mathcal N\left(\frac{\eta \alpha}{\alpha-1}, \frac{\eta^2 \alpha}{(\alpha-1)^2(\alpha-2)}\right)\]

ヒストグラムと, この正規分布の密度関数を同じグラフにプロットして, 比較せよ.

[9]:

# 解答例 3.5
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.stats


b = 4
scl = 1

m_mean = scl * b / (b - 1)
var_mean = scl**2 * b / (b - 1)**2 / (b - 2)
print(m_mean)
n_rep = 10000
n_sizes = [5, 50, 500]
df = pd.DataFrame()
vals = np.linspace(0, 3)
for i_size, n_size in enumerate(n_sizes):
    fig, ax = plt.subplots()
    means = []
    for i_rep in range(n_rep):
        x = scipy.stats.pareto.rvs(b, scale=scl, size=n_size)
        means.append(x.mean())
    cind = str(n_size)
    df[cind] = means
    df[cind].hist(alpha=.5, bins=50, density=True, ax=ax)

    if i_size == 0:
        xps = np.linspace(.5, 2.3)
    elif i_size == 1:
        xps = np.linspace(1, 1.8)
    elif i_size == 2:
        xps = np.linspace(1.2, 1.46)
    fps = scipy.stats.norm.pdf(xps, m_mean, scale=(var_mean/n_size)**0.5)
    ax.plot(xps, fps)

df.describe()

1.3333333333333333

[9]:

	5	50	500
count	10000.000000	10000.000000	10000.000000
mean	1.335572	1.333067	1.332987
std	0.215275	0.067547	0.021253
min	1.030085	1.141187	1.265909
25%	1.194781	1.286677	1.318376
50%	1.287094	1.325433	1.331992
75%	1.415208	1.370448	1.346358
max	5.062055	2.013717	1.439125