Change in amount of heat (enthalpy)

• We assume that the system is at a constant pressure.

  \[\text{(temperature rise)} = \frac{\text{(increase in amount of heat)}}{\text{(heat capacity)}}\]
  \[\Delta T = \frac{\Delta H}{C_p}\]

  where the units of the values are \(C_p\) \(\mathrm{[J \ K^{-1}]}\), \(\Delta H\) \(\mathrm{[J]}\), \(\Delta T\) \(\mathrm{[K]}\).

  Equivalently,

  \[\Delta H = C_p \Delta T\]

• For the system with volume \(V\) and density \(\rho\), and the heat capacity per unit mass \(C_p\) \(\mathrm{[J \ K^{-1} \ kg^{-1}]}\)

  \begin{align*} & \rho V C_p \frac{\partial T}{\partial t} \\ & = \text{rate of }\left( {\bf input} - {\bf output} + \text{production} - \text{consumption} \right) \end{align*}

Example 1

• Consider a steal lod of some length, and suppose we heat up one end of it.

• Then, the heat moves from that end toward the other end, and the temperature (distribution) in the lod will change.

• Derive the equation describing the local temperature change in the rod from the heat balance.

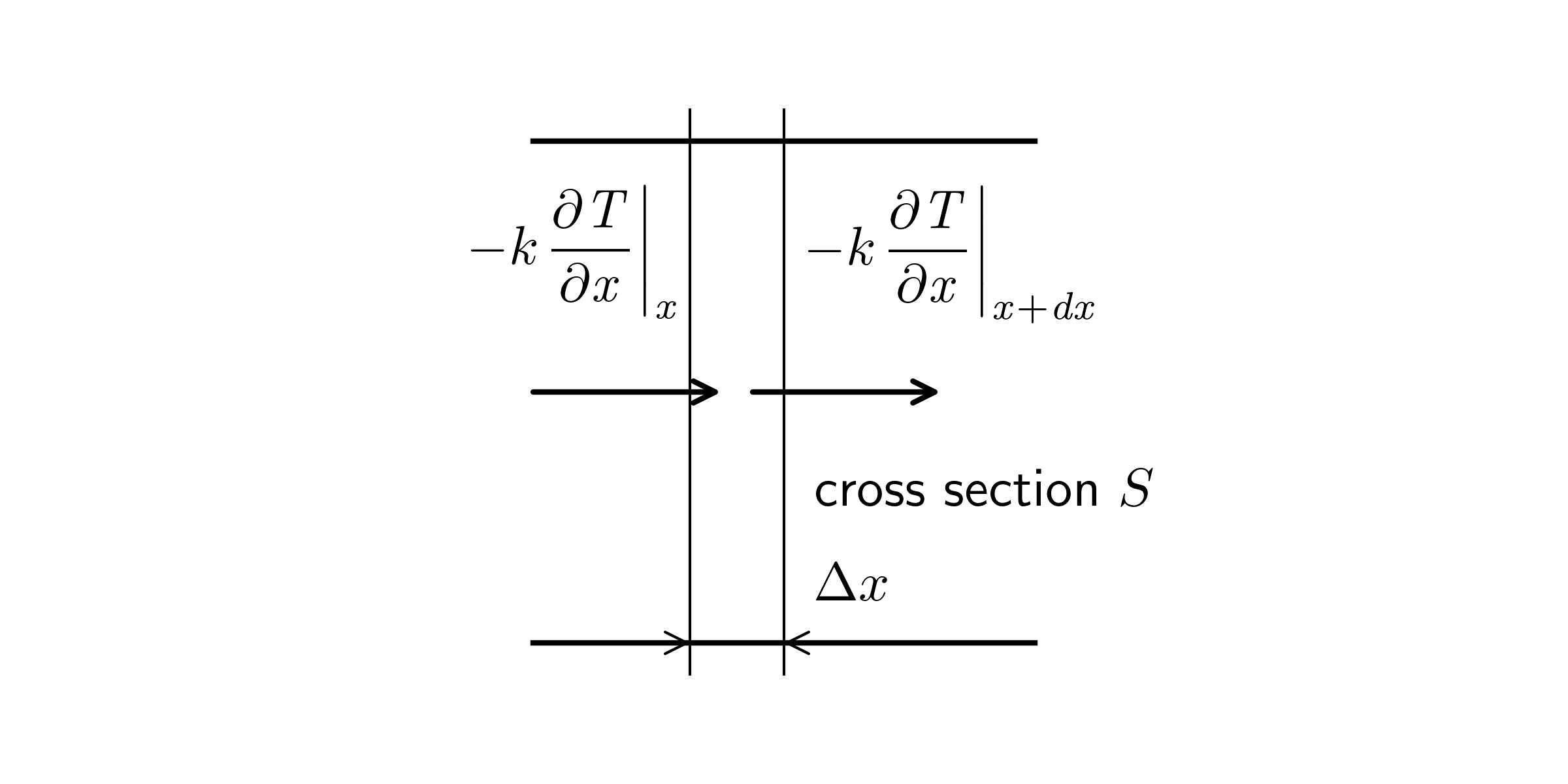
Example 1, solution

• At \(x\)

  \[\text{heat flux} = -k \left. \frac{\partial T}{\partial x}\right\vert_x\]

  the direction is ‘into the system’.

• We call \(\left.\frac{\partial T}{\partial x}\right\vert_x\) the heat gradient at \(x\).

• At \(x + \Delta x\)

  \[\text{heat flux} = - k \left. \frac{\partial T}{\partial x}\right\vert_{x + \Delta x}\]

  the direction is ‘out of the system’.

• Thus,

  \[{\bf input} = S \left( - k \left.\frac{\partial T}{\partial x}\right\vert_x\right)\]
  \[{\bf output} = S \left( - k \left.\frac{\partial T}{\partial x}\right\vert_{x + \Delta x} \right)\]

• The balance is

  \[(\rho S \Delta x) C_p \frac{\partial T}{\partial t} = - S k \left.\frac{\partial T}{\partial x} \right\vert_x - S\left( - k\left. \frac{\partial T}{\partial x} \right\vert_{x + \Delta x} \right)\]

Taking the limit \(\Delta t \to 0\) and \(\Delta x \to 0\), and we have

\begin{equation} \frac{\partial T}{\partial t} = \frac{k}{\rho C_p} \frac{\partial^2 T}{\partial x^2} \tag{a} \label{eq: heat balance} \end{equation}

Quiz 1

• What kind of differential equation is the Eq. \eqref{eq: heat balance}?

Comment

• We discuss the method of solution of Eq. \eqref{eq: heat balance} later in this course.

Example 2

1. Derive the partial differential equation for the radial heat conduction in the pipe. (Radial version of Eq. (a)).

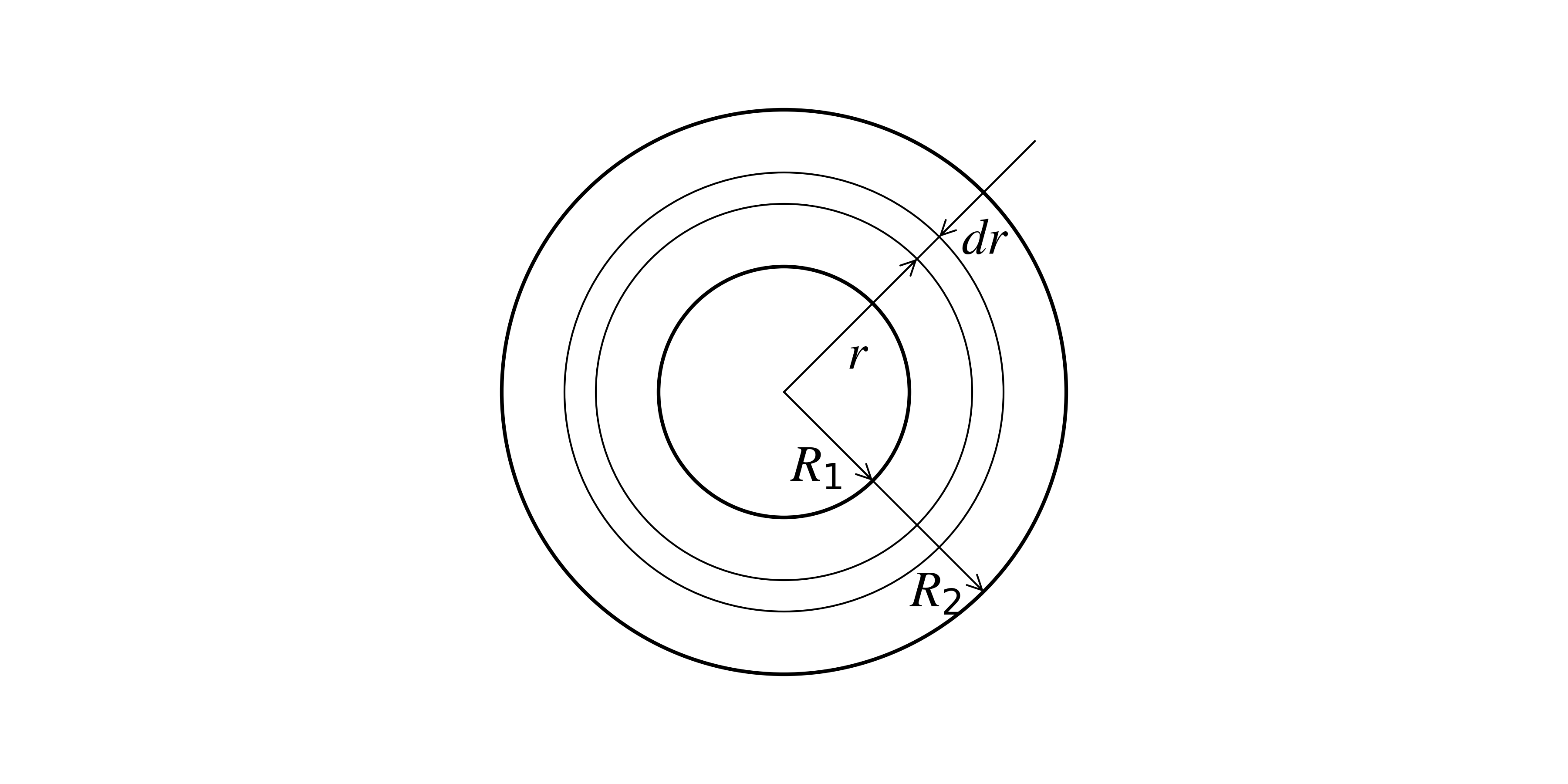
Example 2, solution

• 内径 \(2R_1\), 外径 \(2R_2\) のパイプに, 中心から半径 \(r\) のところに, 厚さ \(dr\) の微小部分を考える. パイプの長さを \(L\) とすると, この微小部分の体積は \(2 \pi r dr L\) で表される.

• 半径 \(r\) の位置でのこの微小体積への熱の流入速度は,

  \[q = \underbrace{(2\pi rL)}_{\text{面積}}\left( - k \left.\frac{\partial T}{\partial r}\right\vert_r \right)\]

• 半径 \(r+dr\) の位置でこの微小体積からの熱の流出速度は,

  \[q = \underbrace{(2\pi (r+ dr) L)}_{\text{面積}}\left( - k \left.\frac{\partial T}{\partial r}\right\vert_{r+dr} \right)\]

• 伝導物質の密度を \(\rho\), 質量当りの（定圧）熱容量を \(C_p\) とすると, 熱収支より,

  \begin{align*} {\rho}{C_p} (2 \pi r drL) \frac{\partial T}{\partial t}& = (2\pi rL)\left( - k \left.\frac{\partial T}{\partial r}\right\vert_r \right) \\ & \quad - {(2\pi (r+ dr) L)}\left( - k \left.\frac{\partial T}{\partial r}\right\vert_{r+dr} \right) \end{align*}

• 両辺を \(\rho C_p 2 \pi r drL\) で割って整理

  \[\frac{\partial T}{\partial t} = \frac{k}{\rho C_p dr} \left( \left. \frac{\partial T}{\partial r} \right\rvert_{r+dr} - \left. \frac{\partial T}{\partial r} \right\rvert_r \right) + \frac{k}{r} \left.\frac{\partial T}{\partial r}\right\rvert_{r+dr}\]

  • \(dr \to 0\) の極限をとって

  \[\frac{\partial T}{\partial t}= \frac{k}{\rho C_p} \left(\frac{\partial^2 T}{\partial r^2} + \frac{1}{r} \frac{\partial T}{\partial r} \right)\]

• 配布資料では, \(\frac{1}{r}\) が \(\frac{2}{r}\) となっていました. 訂正します. (\(\frac{1}{r}\) が正しい).