| ◀ Previous | TOC | Next ▶ |
Linear Partial Differential Equations (Linear PDE)
線形偏微分方程式
What are Partial Differential Equations (PDEs)?
The function to solve has multiple variables.
For example, \(f(x, t)\).
Because \(f\) has multiple variables, we need touse partial derivatives.
Heat Conduction
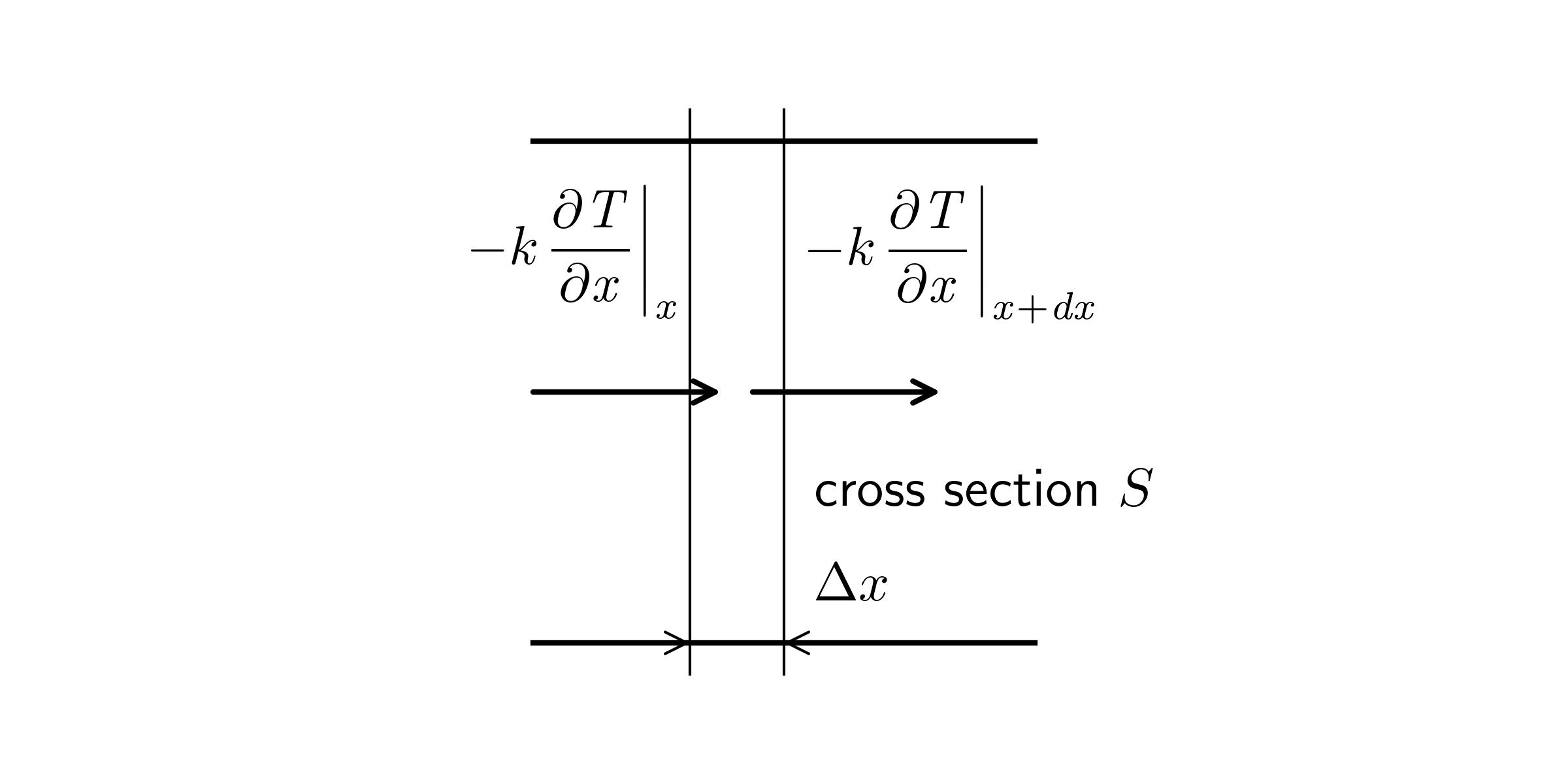
\begin{equation} \frac{\partial T}{\partial t} = \frac{k}{\rho C_p} \frac{\partial^2 T}{\partial x^2} \tag{a} \label{eq: heat balance} \end{equation}
Boundary Value Problems
境界値問題
Example 1
Consider there is a plate whose thickness is \(L\).
For \(t<0\), the inside and the both surfaces of the plate are kept at \(T_h\).
For \(t \ge 0\), the surfaces of the plate are kept at \(T_l\) (\(T_l < T_h\)).
Describe the problem with a partial differential equation (PDE), boundary conditions (BCs), and initial condition (IC).
Derive the dimensionless form of the PDE, BCs and IC.
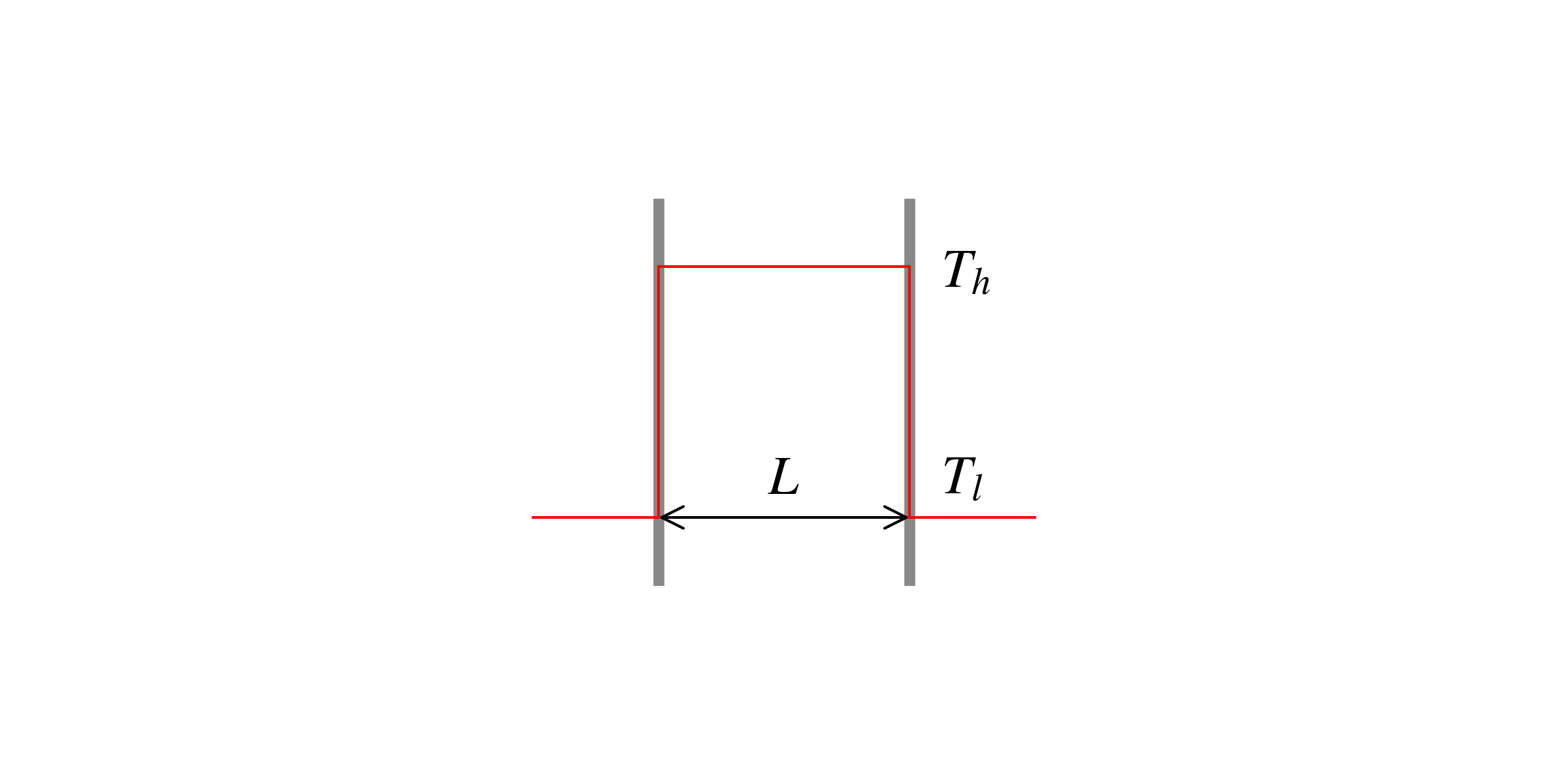
Solution, step 1, find the boundary value problem.
The PDE, boundary conditions (BCs) and initial condition (IC) of this example is
PDE
\begin{equation} \frac{\partial T}{\partial t} = \frac{k}{\rho C_p} \frac{\partial^2 T}{\partial x^2} \label{eq: example 1 pdf} \end{equation}
BCs
\begin{align*} T(0, t) &= T_l \\ T(L, t) &= T_l \end{align*}
IC
\[T(x, 0) = T_h\]
Solution, step 2, simplify the PDE and BCs and IC.
Let
\[u = \frac{T(x, t) - T_l}{T_h - T_l}, \quad p = x / L\]then,
PDE
\[\frac{\partial u(p, t)}{\partial t} = \alpha^2 \frac{\partial^2 u(p, t)}{\partial p^2} \tag{xp.1}\]BCs
\begin{equation} u(0, t) = u(1, t) = 0 \tag{xp.2} \label{eq: DL boundary conditions} \end{equation}
IC
\[u(p, t) = 1 \tag{xp.3}\]
Quiz 1
Find \(\alpha^2\), and its unit (in SI).
Quiz 2
We can make PDE and BCs and IC
i.e., make the coefficient of the right side equal to unity, by changing \(t\) as follows.
Find \(t_0\), and its unit (in SI).
Method of Separation of Variables
Standard method for boundary value problems of partial differential equations.
Assume that \(u(p, s)\) can be expressed as \(u(p, s) = P(p)S(s)\), where \(P(p)\) is a function of only \(p\), and \(S(s)\) is a function of only \(s\).
Rationale: \(u\) should be a linear combination of functions of \(p\), and also a linear combination of functions of \(s\). The only form that satisfies these conditions is \(P(p)S(s)\)
Example 2
Solve the dimensionless problem (D.1)–(D.3) with the MSV.
Solution, step 1, applying the MSV.
\(u(p, s) = P(p)S(s)\), then the PSE is
\[P\frac{d S}{ds} = \frac{d^2 P}{d p^2} S\]Divide the both sides by \(SP\) and we have
\[\frac{1}{S} \frac{d S}{ds} = \frac{1}{P} \frac{d^2 P}{dp^2}\]Note the left side is the function of only \(s\) and the right side is the function of only \(p\). In order to this be true, both left and right sides should be constant.
We let the constant be \(-\lambda^2\)
\[\frac{1}{S} \frac{d S}{ds} = \frac{1}{P} \frac{d^2 P}{dp^2} = - \lambda^2\]The reason why we choose negative value \(-\lambda^2\) for the constant is from the view point of physics, not mathematics.
In this problem, \(u\) should decay over time to 0. For this, we need negative value for the constant.
Solution, step 2, solve the derived ODE.
\begin{align} &\frac{dS}{ds} + \lambda^2 S = 0 \tag{S} \\ & \frac{d^2 P}{dp^2} + \lambda^2 P = 0 \tag{P} \end{align}
The general solution for the ODEs are
\[S = K \exp(-\lambda^2 s)\]\[P = A \cos \lambda p + B \sin\lambda p\]where \(K, A, B\) are arbitrary constants.
The general solution for the PDE is, therefore,
\[u(p, s) = \exp(-\lambda^2 s) \left(A \cos \lambda p + B \sin \lambda p \right) \tag{GS}\]
Solution, step 3, Apply the BCs
Noting that \(\exp(- \lambda^2 s) \ne 0\), we apply (xp. 2) to (GS) and have
\[A = 0, \quad A \cos \lambda + B \sin \lambda = 0\]From these, we have \(A=0\) and
\[\sin \lambda = 0\]That is,
\[\lambda = 0, \pm \pi, \pm 2\pi, \dotsc\]This means,
\[\lambda_n = n \pi, \quad n = -\infty, \dotsc, \infty\]satisfy the BCs.
The general solution satisfying BCs is then
\[u(p, s) = \sum_{n = -\infty}^\infty \exp\left\{-(n \pi)^2 s \right\} B_n \sin (n \pi p) \tag{GS. BC}\]A bit of transformation:
Note that \(\sin (-n \pi p) = - \sin (n \pi p)\),
which means we can conbine the two terms into one with
\[B^\prime_n = B_n - B_{-n}\]Also note for \(n=0\), \(\sin (0 \pi p) = \sin 0 = 0\).
From these, the general solution can be expressed as
\[u(p, s) = \sum_{n = 1}^\infty \exp(-n^2 \pi^2 s) B^\prime_n \sin (n\pi p) \tag{GS. BC 2}\]
Solution, step 4, applying the IC.
Now we get to the hardest part.
\[1 = u(p, 0) = \sum_{n=1}^\infty B^\prime_n \sin (n \pi p)\]We use the Fourier series expansion.
Multiplying the both sides by \(\sin (m \pi p)\) and integrate with respect to \(p\),
\begin{align*} \int_0^1 \sin (m \pi p) \, dp & = \int_0^1 \sum_{n=1}^\infty B^\prime_n \sin(m\pi p) \sin (n \pi p) \, dp \\ & = \sum_{n=1}^\infty \int_0^1 B^\prime_n \sin(m\pi p) \sin (n \pi p) \, dp \tag{FS.A} \end{align*}
\(\sin (n\pi p)\), \(n=1, 2, \dotsc\) are orthoginal functions, that is,
\[\begin{split}\int_0^1 \sin(m \pi p) \sin (n \pi p) \, dp = \begin{cases} \frac{1}{2} & m = n \\ 0 & m \ne n\end{cases}\end{split}\]
The left side o (FS.A) is,
\begin{align*} \int_0^1 \sin (m \pi p) \, dp & = \left[ - \frac{1}{m \pi} \cos (m \pi p) \right]_0^1 \\ & = \begin{cases} \frac{2}{m \pi} & m = 2k - 1 \\ 0 & m = 2k \end{cases}, \text{ for } k = 1, 2, \dotsc, \end{align*}
The right side, for \(m\)
\begin{align*} \sum_{n=1}^\infty \int_0^1 B^\prime_n \sin(m\pi p) \sin (n \pi p) \, dp = \frac{1}{2} B^\prime_m \end{align*}
Finally, we have
\[B_k^\prime = \frac{4}{(2k - 1) \pi}, \quad k = 1, 2, \dotsc,\]
Property of the solution
As \(s \to \infty\), it reduces to
\[\frac{4}{\pi} \exp\left( - \pi^2 s \right) \sin(\pi p)\]Only the term for \(k=1\) survives.
decay of dimensionless (amount of) heat for \(k=1\),
\begin{align*} & \int \frac{4}{\pi} \exp \left(- \pi^2 s \right) \sin (\pi p) \, dp = \frac{4}{\pi}\exp \left(- \pi^2 s \right) \int_0^1 \sin (\pi p) \, dp \\ & = \frac{4}{\pi}\exp \left(- \pi^2 s \right) \underbrace{\left[ - \frac{1}{\pi} \cos (\pi p) \right]_0^1}_{= 2 /\pi} \\ & = \frac{8}{\pi^2} \exp \left(- \pi^2 s \right) \end{align*}
| ◀ Previous | TOC | Next ▶ |