| ◀ Previous | TOC | Next ▶ |
1. 多変数関数の極大・極小問題
Local extremes
内容
極大・極小問題とは
Taylor 展開と Hesse 行列
行列の 2 次形式と固有値, 正定値, 負定値
関数の Hesse 行列の固有値と極大・極小
1.1 極大・極小問題とは
多変数の極大・極小問題は 1 変数のそれより数段難しい.
まずは 1 変数の復習から.
\[y = x^3 - 2 x^2 + x\]は 極大と極小を持つ.
極大値, 極小値では, \(f^\prime(x) = 0\), 極大値で \(f^{\prime\prime}(x) < 0\), 極小値で \(f^{\prime\prime}(x) > 0\) となる.
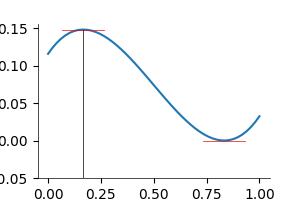
では, 2 変数ではどうか.
例題 1.1
関数 \(z = x^2 + y^2 - 3xy\) は極値をとるか?
例題 1 考え方
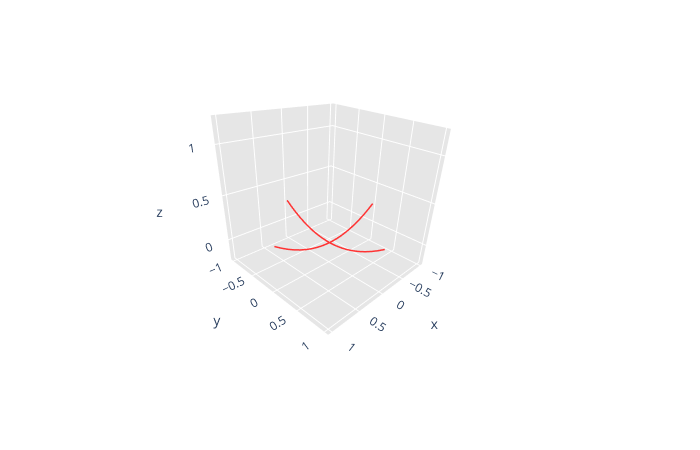
例えば, \(z = x^2 + y^2 - 3xy\) のグラフを, \(y=0\) 断面と \(x=0\) 断面で表示すると,
次のグラフのように, この 2 つのグラフは, \((x, y) = (0, 0)\) で極小となっている.
では, \((x, y) = (0, 0)\) は \(z = x^2 + y^2 - 3xy\) の極小点か.
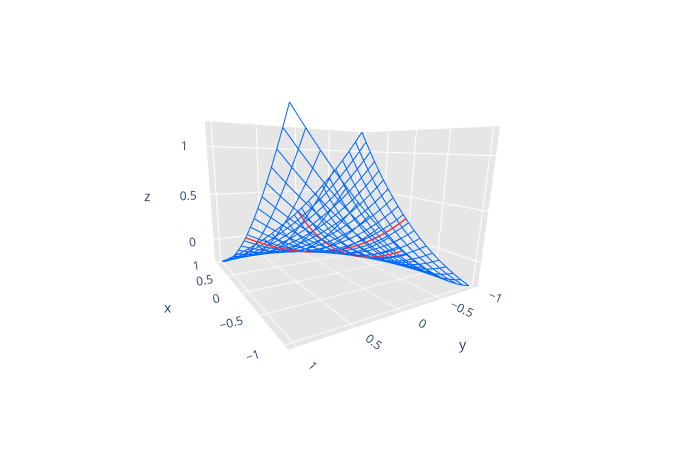
実は, \(z = x^2 + y^2 - 3xy\) のグラフは次のようになっている. * \((x, y)= (0, 0)\) はこの関数の極小点ではない. 鞍点(saddle point)である.
解答 1.1
極値を持たない.
より一般的な解答については以下の解説を参照されたし.
多変数の極大・極小の難しさ
極値をとるためには, その点を通るあらゆる方向(360 度)の直線上で, (1 変数の意味で)極大あるいは極小とならなければならない.
\(n\) 変数の場合どうするか.
解析的手法だけでは大変.
線形代数を用いる.
多変数の極大・極小問題の解き方
考えている範囲で関数は 2 回連続微分可能(twice continuously differentiable)であるとする.
停留点を求める(Q, 停留点の定義は?).
停留点での Hesse 行列を求める.
Hesse 行列の固有値を求める.
固有値がすべて正であれば極小値, 固有値がすべて負であれば極大値.
1.2 なぜ Hesse 行列 (Hessian Matrix) を用いるのか.
Taylor 展開
Taylor 展開について注意
たいていの場合、必要なのは 1 次, あるいは 2 次までの展開である.
剰余項が問題になることはまれで, 多くの場合, これについてはオーダー(ランダウの big-\(O\), little-\(o\) など)だけを考えればよい.
やってみると, Taylor 展開は意外に面倒くさくない.
ここで学ぶこと
2 変数の Taylor 展開を 2 次の項まで.
ヘッセ行列 (Hessian matrix).
例題 1.2
関数 \(z= f(x, y)\), \(x, y, z \in \mathbb R\) が少なくとも 2 回連続微分可能であるとする.
このとき, \(z = f(x, y)\) の (1) 1 次までと, (2) 2 次までの Taylor 展開を示せ.
但し, 剰余項は, ランダウの big-\(O\) によるオーダーを示すだけでよい.
解答 1.2
(1) 1 次までの展開
\begin{align*} &f(x + \Delta x, y + \Delta y) \\ \quad &= f(x, y) + \frac{\partial f}{\partial x}(x, y) \Delta x + \frac{\partial f}{\partial y}(x, y) \Delta y + O(h^2) \end{align*}
(2) 2 次までの展開
\begin{align*} &f(x + \Delta x, y + \Delta y) = f(x, y) %\\ & \quad + \frac{\partial f}{\partial x} (x, y) \Delta x + \frac{\partial f}{\partial y} (x, y) \Delta y \\ & \quad + \frac{1}{2} \left\{ \frac{\partial^2 f}{\partial x^2}(x, y) (\Delta x)^2 + 2\frac{\partial^2 f}{\partial x \partial y}(x, y) \Delta x \Delta y + \frac{\partial^2 f}{\partial y^2}(x, y) (\Delta y)^2 \right\} \\ & \quad + O ( h^3) \end{align*}
定理 1.1
次式が成立するためには, \(\partial^2 f / \partial x \partial y\) と \(\partial^2 f / \partial y \partial x\) が存在し, かつ, ともに \((x, y) = (a, b)\) において連続であることが十分である.
Quiz
「1 変数関数が \(k\) 回連続微分可能」について
1 年生で使った教科書にどのように記述されているか調べよ(記述がない場合もあり得る).
「\(n\) 変数関数が \(k\) 回連続微分可能」についてはどうか.
例題 1.3
関数 \(z = f(x, y)\) が \((a, b)\) をふくむある開領域で 2 回連続微分可能であれば, 式 (1.1) が成立することを示せ.
解答 1.3
関数が \(z = f(x, y)\) が 2 回連続微分可能ということは, \(f\) の 2 階導関数がすべてが存在して, かつ連続であるということである.
\((a, b)\) を含むある開領域で 2 階連続微分可能であるということは, \((a, b)\) で上記の導関数が連続である, ということである.
したがって, 定理 1.1 より, (1.1) が成り立つ.
\((a, b)\) を含む開領域で 2 回連続微分, ということは, この領域が \((a, b)\) を境界点ではなく, 内点として含む, ということを保証している. この部分は講義の範囲を越えており, あまり気にしなくて良い.
例題 1.4
\(z = x^2 + y^2 - 3xy\) を 2 次まで Taylor 展開せよ.
解答 1.4
1 次までの展開
\begin{align*} &f(x + \Delta x, y + \Delta y = f(x, y) \\ & \quad + (2 x - 3 y) \Delta x + (- 3x + 2y) \Delta y + O(\Delta x^2 + \Delta y^2) \end{align*}
2 次までの展開
\begin{align*} &f(x + \Delta x, y + \Delta y = f(x, y) \\ & \quad + (2 x - 3 y) \Delta x + (- 3x + 2y) \Delta y \\ & \quad + \frac{1}{2} \left\{ 2 \Delta x^2 - 6 \Delta x \Delta y + 2 \Delta y^2 \right\} + O((\Delta x^2 + \Delta y^2)^{3/2}) \end{align*}
極小値をとるための条件
\((x, y) = (a, b)\) が極小値をとるためには,
条件 1: 停留点
条件 2: 正値性
\(\Delta x \ne 0\) または \(\Delta y \ne 0\) に対して
定理 1.2
\((x, y)=(a, b)\) が極小値を与えるためには, 上記の条件 1 かつ条件 2 が必要十分である.
Remark
2 変数の場合は, 2 次関数の判別式を用いても解ける.
\(a = \frac{\partial^2 f}{\partial x^2}\), \(b = \frac{\partial ^2 f}{\partial x \partial y}\), \(c = \frac{\partial^2 f}{\partial y^2}\) とおく.
このとき, (4) の左辺は以下のようになる.
\[g = a (\Delta x)^2 + 2b (\Delta x)(\Delta y) + c (\delta y)^2\]さて, \(D = b^2 - ac <0\) ならば, \(g = 0\) に解はない. つまり常に \(g > 0\) あるいは常に \(g < 0\).
したがって, \(a > 0\) のとき \(g > 0\), \(a < 0\) のとき, \(g < 0\).
すなわち, 方程式 \(g=0\) の判別式 \(D < 0\) かつ \(a>0\) のとき, 極小値をもち, \(D <0\) かつ \(a<0\) のとき, 極大値をもつ.
However, this method cannot be applied if the dimension of the matrix is greater than 2.
Question
変数の数が 2 より大きい場合(\(n\) 変数, \(n>2\))どうするか?
線形代数を使う必要がある.
Hesse 行列(Hessian matrix)
\[\begin{split}H = \begin{bmatrix} \dfrac{\partial^2 f}{\partial x^2} & \dfrac{\partial^2 f }{\partial x \partial y} \\ \dfrac{\partial^2 f}{\partial x \partial y} & \dfrac{\partial^2 f}{\partial y^2} \end{bmatrix}\end{split}\]線形代数より, \(H\) の固有値が全て正であれば, 次が成立する.
Remark
英語で単に Hessian といえば, Hesse 行列の行列式になる.
まとめ
条件 2 は, \(n\) 次元では次のようになる.
これは, 線形代数の用語では, 行列 \(H\) の 2 次形式が正である,
あるいは, 行列 \(H\) が正定値(positive definite)であるという.
行列 \(H\) が正定値であることと, \(H\) の固有値がすべて正であることとは同値.
1.3 行列の正値性, 2 次形式
2 次形式
例題 1.5
次の \(A\), \(\boldsymbol b\) について, \(Q(\boldsymbol x) = \boldsymbol x^\mathrm T A \boldsymbol x\) を求めよ.
解答 1.5
対称行列については以下が成立(覚えること)
対称行列 \(A\) は直交行列 \(P\) により必ず対角化できる.
\[J = P^{-1} A P\]直交行列においては,
である. すなわち
行列, ベクトルの計算上の重要なルール(覚えること)
ものすごく役に立つ.
というよりは, このルールを使わないと応用で線形代数を使うのは難しい.
これは, \(A\), \(B\) が正方行列でなくても成立する.
\(A\) が \(l \times m\) 行列, \(B\) が \(m \times n\) 行列のとき
\(AB\) は \(l \times n\) 行列.
\(B^\mathrm T\) は \(n \times m\) 行列, \(A^\mathrm T\) は \(m \times l\) 行列だから, \(B^\mathrm T A^\mathrm T=(AB)^\mathrm T\) は \(n \times l\) 行列
行列とベクトルの積の転置については
\[(A \boldsymbol b)^\mathrm T = b^\mathrm T A^\mathrm T \tag{1.3}\]
例題 1.6
次の場合に, 式 (1.3) を確かめよ.
解答 1.6
\begin{align*} \boldsymbol b^\mathrm T A^\mathrm T & = \begin{bmatrix}x, \quad y \end{bmatrix}\begin{bmatrix} a & c \\ b & d \end{bmatrix} = \begin{bmatrix} xa + yb, \quad xc + yd \end{bmatrix} \\ & = \left[ ax + by, \quad cx + dy \right] \end{align*}
したがって
ここで
とおくと,
2 次元の場合で考えると
\(\boldsymbol \xi\) \(=\) \([\xi_1, \xi_2]^\mathrm T\),
このとき
\begin{align*} Q(\boldsymbol x) & = \xi_1 \lambda_1 \xi_1 + \xi_2 \lambda_2 \xi_2 \\ & = \lambda_1 \xi_1^2 + \lambda_2 \xi_2^2 \end{align*}
ここから分かるように, \(\lambda_1 > 0\) かつ \(\lambda_2 > 0\) のとき,
これは, \(A\) の固有値のみで決まる. このような行列を正定値という.
半正定値, 負定値, 半負定値も覚える.
極値問題への応用
2 変数関数 \(z = f(x, y)\) の停留点 \((x, y) = (a, b)\),
\[\frac{\partial f}{\partial x}(a, b) = \frac{\partial f}{\partial y}(a, b) = 0\]Hesse 行列
\[\begin{split}H = \begin{bmatrix} \dfrac{\partial^2 f}{\partial x^2} & \dfrac{\partial^2 f}{\partial x \partial y} \\ \dfrac{\partial^2 f}{\partial x \partial y} & \dfrac{\partial^2 f}{\partial y^2} \end{bmatrix}\end{split}\]が正定値であれば, 任意のベクトル \(\Delta \boldsymbol x = [\Delta x, \Delta y]^\mathrm T\) に対して, 2 次形式
\[Q(\Delta \boldsymbol x) = (\Delta \boldsymbol x)^ \mathrm T H \Delta \boldsymbol x\]は常に正, すなわち, \((x, y) = (a, b)\) は極小値となる.
すなわち, Hesse 行列 \(H\) の固有値がすべて正の場合, \((x, y) = (a, b)\) は極小値となる.
1.4 学習の参考に
応用で使う場合, 行列式, 固有値固有ベクトル, 2 次形式, 線形空間の性質, が重要.
線形代数を復習する場合, 応用上で出てきたトピックスに対して, 関連する部分を復習するのがよい.
今回の講義に関しては, 2 次形式はもちろん, 転置, 対称行列, 直交行列.
1 年生で使った教科書が 2 次形式までしっかりと解説してあればよいが, そうでない場合は, もう少し高度なテキストが必要
インターネット上のサイトをテキスト代わりに使う.
線形代数の教科書は山ほどあるが, 1 年生の線形代数の次のステップに進むためのものとして, 例えば
児玉慎三, 須田信英, システム制御のためのマトリクス理論, コロナ社, 1978. https://www.coronasha.co.jp/np/isbn/9784339083309/
笠原皓司, 新装版改訂増補, 線形代数と固有値問題–スペクトル問題を中心に, 現代数学社, 2019. https://www.gensu.co.jp/book_print.cgi?isbn=978-4-7687-0519-3
- 洋書では, Strang, G, Introduction to linear algebra, 5th Ed., Cambridge University Press, 2016.
この本は, 邦訳も出ている(ただし, 第 4 版). 洋書も邦訳も自然科学系図書館にある.
著者の MIT インターネット講義のサイトは大人気. 工学のいろんな分野の学生・研究者が著者のサイトで学んでいる.
その意味で, 間違いなく世界標準である.
この本は通読してもよいと思う.
| ◀ Previous | TOC | Next ▶ |