連立線形微分方程式（線形微分方程式系）

• \(\boldsymbol x = [x_1, \dotsc, x_n]^\mathrm T\) に関する 1 階の微分方程式, 初期値問題 \(\boldsymbol x(0) = \boldsymbol x_0\).

\begin{equation} \begin{bmatrix}\frac{d x_1}{dt} \\ \vdots \\ \frac{d x_n}{dt}\end{bmatrix}=\begin{bmatrix}a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots　\\ a_{n1} & \cdots & a_{nn}\end{bmatrix}\begin{bmatrix}x_1 \\ \vdots \\ x_n\end{bmatrix},　\quad \boldsymbol x(0)= \boldsymbol x_0=\begin{bmatrix}x_{1,0} \\ \vdots \\ x_{n, 0}\end{bmatrix}, \tag{2.2} \end{equation}

• 記号 \({\cdot}^\mathrm T\) はベクトルや行列の転置（transpose）を表す. \([x_1, \dotsc, x_n]^\mathrm T\) は横ベクトルの転置だから縦ベクトルになる.

1 変数線形微分方程式と微分方程式系の初期値問題と解の比較

• 1 変数線形微分方程式 （\(x, x_0, t \in \mathbb R\), \(a\) は定数）

  \[\frac{d x}{d t} = a x, \quad x(0) = x_0 \tag{2.3}\]

  解は

  \[\quad x = x_0 e^{at} = e^{at} x_0\]

• 線形微分方程式系 （\(\boldsymbol x, \boldsymbol x_0 \in \mathbb R^n\), \(t \in \mathbb R\), \(A\) は定数行列）

  \[\frac{d \boldsymbol x}{d t} = A \boldsymbol x, \quad \boldsymbol x(0) = \boldsymbol x_0\]

  解は

  \[\boldsymbol x(t) = \underbrace{e^{At}}_{\text{行列}}\underbrace{\boldsymbol x_0}_{\text{ベクトル}} \tag{2.4}\]

• \(e^{At}\) ?

行列の指数関数の定義（matrix exponential）

• 復習: 指数関数の定義

• 注意: 指数関数の定義の仕方はひとつではない.

  \begin{align*} e^a & (= \exp a) =\sum_{k=0}^\infty \frac{a^k}{k!} \\ & = 1 + a + \frac{1}{2} a^2 + \frac{1}{6} a^3 + \dotsb \tag{2.5} \end{align*}

定義 2.1 （行列の指数関数）

• \(A\) を \(n \times n\) 行列とするとき 　\begin{align*} e^A & (= \exp A) = \sum_{k=0}^\infty \frac{A^k}{k!} \\ & = E + A + \frac{1}{2}A^2 + \frac{1}{6} A^3 + \dotsb \tag{2.6} \end{align*}

  ここで \(E\) は単位行列である.

対角行列の指数関数

• \(A\) が対角行列 \(D\) のとき

  \[\begin{split}D = \begin{bmatrix} d_1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & d_n \end{bmatrix}\end{split}\]

• \(e^{tD}\) は

  \[\begin{split}e^{tD} = \begin{bmatrix} e^{t d_1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & e^{td_n} \end{bmatrix}\end{split}\]

行列の指数関数の計算 1: 行列の対角化（復習）

• \(A \in \mathbb R^{n\times n}\) が対角化できるとき,

  対角化行列 \(J\) は, 列固有ベクトルを並べた行列 \(P\) を用いて次のように表される.

  \[J = P^{-1} A P\]

• 復習: 行列のべき, 行列の対角化・標準化

行列の指数関数の計算 2: 対角化行列のべき

定理 2.1

• \(A \in \mathbb R^{n\times n}\) が \(J\) に対角化されるとき,

\begin{align*} J^n = P^{-1} A^n P \end{align*}

証明

\begin{align*} J^n &= (P^{-1} A P)^n \\ & = \underbrace{ (P^{-1} A \underbrace{P)(P^{-1}}_{E} A P) \dotsm (P^{-1} A P) }_n \\ & = P^{-1} A^n P \end{align*}

定理 2.2

• \(A \in \mathbb R^{n\times n}\) が \(J\) に対角化されるとき,

  \[A^n = P J^n P^{-1}\]

行列の指数関数の計算3: 行列の指数関数の対角化

定理 2.3

• \(n \times n\) 実数行列 \(A\) （\(A \in \mathbb R^{n \times n}\)）が \(J= P^{-1} A P\) と対角化可能なとき,

• 補足: \(t\) がスカラー（scalar) のとき, \(e^{tA} = e^{At}\) である. どちらの表記も可.

定理 2.3 の証明

\begin{align*} e^{tJ} &= e^{(P^{-1} A P) t} \\ & = E + (P^{-1} A P) t + \frac{(P^{-1}A P)^2 t^2}{2!} + \dotsb + \frac{(P^{-1} A P)^k t^k}{k!} + \dotsb \\ & = P^{-1} E P + P^{-1} (At) P + \frac{P^{-1} A^2 t^2 P}{2!} + \dotsb + \frac{P^{-1} A^kt^k P}{k!} + \dotsb \\ & = P^{-1} \left( E + At + \frac{A^2 t^2}{2!} + \dotsb + \frac{A^k t^k}{k!} + \dotsb\right) P \\ & = P^{-1} e^{tA} P \end{align*}

行列の指数関数の対角化

• 線形系の解が以下のとおりとする.

  \[\boldsymbol x = e^{tA} \boldsymbol x_0 = P \underbrace{e^{tJ}}_{t \textbf{ 依存はここだけ}} P^{-1} \boldsymbol x_0\]

• このとき, \(e^{tJ}\) は, \(J\) が対角行列なので

  \[\begin{split}e^{tJ} = \begin{bmatrix} e^{\lambda_1 t} & 0 &\cdots & 0\\ 0 & e^{\lambda_2 t} &\cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & e^{\lambda_n t} \end{bmatrix}\end{split}\]

行列 \(A\) の固有値が実数の場合

• 固有値 \(\lambda_i\) に対する \(e^{t\lambda_i}\) の挙動

  \[\lambda_i > 0 \quad \Rightarrow \quad e^{\lambda_i t} \to \infty \quad \text{ as } t \to \infty,\]
  \[\lambda_i = 0 \quad \Rightarrow \quad e^{\lambda_i t} = 1\]
  \[\lambda_i < 0 \quad \Rightarrow \quad e^{\lambda_n t} \to 0 \quad \text { as } t \to \infty.\]

• 線形システムの挙動は固有値で決まってしまう.

例題 2.1

• 次の \(A\), \(\boldsymbol x_0\) に対して, \(\boldsymbol x= e^{tA} \boldsymbol x_0\) は \(t \to \infty\) でどのようになるか.

解答例 2.1

• \(\boldsymbol x\) は次のように表される.

  \[\begin{split}\boldsymbol x = \begin{bmatrix} e^{2t} \\ e^{-t} \end{bmatrix}\end{split}\]

• すなわち, \(\boldsymbol x = [x_1, x_2]^\mathrm T\) とすると, \(x_1\) は無限大に発散し, \(x_2\) は 0 に近づく.

行列 \(A\) の固有値と \(e^{tA}\) （固有値が実数の場合）, まとめ

• 行列があるベクトルに作用するとき, そのベクトルを固有ベクトルの方向に固有値倍する.

• \(A\) の固有値がすべて負であれば, \(e^{tA} \to \boldsymbol 0\).

• 固有値がすべて 0 であれば, 変化はない.

  \[e^{tA}=P e^\boldsymbol 0 P^{-1} = P E P^{-1} = E\]

• 固有値 \(\lambda_i\) が正の成分は発散する. すなわち, 系は固有ベクトル \(\boldsymbol p_{\lambda_i}\) の方向に無限大に向かう.

• 系が発散しないためには, すべての固有値に対し,

  \[\lambda_i \le 0\]

  であることが必要十分である.

例題 2

• 次の微分方程式の解を \(x\)-\(y\) 平面上に描け.

解答例

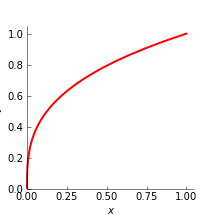
例題 2.3

• 例題 2.2 の微分方程式の相図を描け.

解答例 2.3（相図）

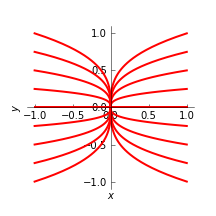
復習

• 行列

  • 行列式, トレース, 固有値, 固有ベクトル

  • 対角化可能性

    • まともにやると大変.

    • 対称行列が直交行列で対角化できることは覚えておくこと.

  • 2 次元正則行列の逆行列. \(A\) を \(2 \times 2\) 実数値正則行列とする.

    \[\begin{split}A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \quad \Rightarrow \quad A^{-1} = \frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}\end{split}\]

• Euler の公式

  \[e^{\pm i\theta} = \cos \theta \pm i \sin \theta\]

  または

  \[\cos \theta = \frac{e^{i \theta} + e^{-i\theta}}{2}, \quad \sin \theta = \frac{e^{i \theta} - e^{-i\theta}}{2i}\]

共役複素数の固有値

• 次の行列を定義する.

  \[\begin{split}E = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, \quad K = \begin{bmatrix} i & 0 \\ 0 & -i \end{bmatrix}\end{split}\]

• 実数行列の固有値は, 実数か共役複素数. \(a, b \in \mathbb R\) として

\begin{align*} J & = \begin{bmatrix} a + b i & 0 \\ 0 & a - b i \end{bmatrix} \\ & = \begin{bmatrix} a & 0 \\ 0 & a \end{bmatrix} + \begin{bmatrix} bi & 0 \\ 0 & - bi \end{bmatrix} \\ & = a E + b K \end{align*}

• このとき,

  \[e^{tJ} = \underbrace{e^{taE}}_{\text{大きさ}} \underbrace{e^{tbK}}_{\text{回転}}\]

• つまり, 固有値の実部は大きさの変化を, 虚部は回転の度合いを表す.

• ただし, \(e^{tbK}\) が実数行列になるためには, 基底変換が必要である.

行列 \(A\) の固有値と \(e^{tA}\)

• \(A\) の固有値の実部がすべて負であれば, \(e^{tA} \to \boldsymbol 0\)（零行列）.

• 固有値がすべて 0 であれば, 変化はない.

• 固有値 \(\lambda_i\) の実部が正の成分は発散する. すなわち, 系は固有ベクトル \(\boldsymbol p_{\lambda_i}\) の方向に無限大に向かう.

• 系が発散しないためには, すべての固有値に対し,

  \[\mathrm{Re}(\lambda_i) \le 0\]

  であることが必要十分である. （\(\mathrm{Re}\) は複素数の実部をとる関数.）

• 実行列の固有値が虚数の場合, 必ず共役複素数のペアになるが, その虚部は, 回転の大きさに関係する.

行列が対角化できて固有値が全て実数の場合

• 行列が次の行列の形をしている時の \(\boldsymbol x = e^{tA} \boldsymbol x_0\)

• \(a_{22}\) の \(-1\) を \(1\) に変えると, 時間について反転.

• 固有ベクトルは \([1, 0]^\mathrm T\), \([0, 1]^\mathrm T\).

• \(a<0\) のとき, \(e^{tA} \boldsymbol x_0\) は \([0, 0]^\mathrm T\) に収束.

  • \(a<-1\) のとき, \(x\) 軸の収束のほうが \(y\) 軸より速い.

  • \(a = -1\) のとき, 同じ速度で収束するので, 相図は放射状になる.

  • \(-1 < a < 0\) のとき, \(y\) 軸の収束のほうが \(x\) 軸より速い.

• \(a = 0\) のとき, \(x\) 軸は変化せず, \(y\) 軸は \(0\) に収束.

• \(a > 0\) のとき, \(x\) 軸は発散, \(y\) 軸は \(0\) に収束.

行列が対角化できて固有値が全て実数の場合の相図

行列が対角化できて行列の固有値が共役複素数の場合

• 次の行列の時の \(\boldsymbol x = e^{tA} \boldsymbol x_0\)

• \(a< 0\) ならばうずまきながら \([0, 0]^\mathrm T\) に収束する.

• \(a = 0\) ならば回転する（固有値が純虚数）.

• \(a> 0\) ならばうずまきながら発散する.

行列が対角化できて固有値が共役複素数の場合の相図