5.1 行列の指数関数の計算

[1]:

# scipy.linalg.expm の例
import scipy.linalg


a = [[-1, -1], [1, -2]]
ea = scipy.linalg.expm(a)
print(ea)

[[ 0.24269012 -0.19626633]
 [ 0.19626633  0.04642379]]

5.2 線形微分方程式系の観点からの行列の分類

5.3 行列が対角化できて固有値が全て実数の場合

• 行列が次の形とする.

• \(a_{22}\) の \(-1\) を \(1\) に変えると, 時間について反転.

• 固有ベクトルは \([1, 0]^\mathrm T\), \([0, 1]^\mathrm T\).

• \(a<0\) のとき, \(e^{tA} \boldsymbol x_0\) は \([0, 0]^\mathrm T\) に収束.

  • \(a<-1\) のとき, \(x\) 軸の収束のほうが \(y\) 軸より速い.

  • \(a = -1\) のとき, 同じ速度で収束するので, 相図は放射状になる.

  • \(-1 < a < 0\) のとき, \(y\) 軸の収束のほうが \(x\) 軸より速い.

• \(a = 0\) のとき, \(x\) 軸は変化せず, \(y\) 軸は \(0\) に収束.

• \(a > 0\) のとき, \(x\) 軸は発散, \(y\) 軸は \(0\) に収束.

\(a=-2\)

\(a=-1\)

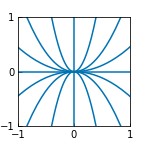
\(a=-0.5\)

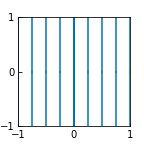
\(a=0\)

\(a=1\)

5.4 行列が対角化できて行列の固有値が共役複素数の場合

• \(a< 0\) ならばうずまきながら \([0, 0]^\mathrm T\) に収束する.

• \(a = 0\) ならば回転する（固有値が純虚数）.

• \(a> 0\) ならばうずまきながら発散する.

\(a < 0\)

\(a=0\), 固有値が純虚数

\(a>0\)

5.5 行列が対角化できない場合（固有値が縮退している場合）

• 行列は Jordan 標準形

• 固有ベクトルは \([1, 0]^\mathrm T\) のみ.

\(a=-1\)

5.6 軌跡の表示

• 次の行列について, \(e^{tA}\) を考える.

[28]:

#### 初期値 [1, 3]^T のときの x(t), y(t)

import matplotlib.pyplot as plt
import numpy as np
import scipy.linalg


a = np.array([[-3.,  1.], [ 1., -3.]])
print('a = ',  a)
eigval, eigvec = np.linalg.eig(a)
print('a eigval', eigval)
print('a eigvec\n', eigvec)

x_0 = np.array([[1], [3]])

ts = np.linspace(0, 3)
xs = []
for t in ts:
    eta = scipy.linalg.expm(t * a)
    x = np.matmul(eta, x_0)
    xs.append(x)

xs = np.array(xs)

fig0, ax0 = plt.subplots()
ax0.set_yscale('log')
ax0.plot(ts, xs[:, 0])
ax0.plot(ts, xs[:, 1])

fig1, ax1 = plt.subplots(figsize=(4,4))
ax1.plot(xs[:, 0], xs[:, 1])
ax1.set_xlim(0, 3)
ax1.set_ylim(0, 3)

a =  [[-3.  1.]
 [ 1. -3.]]
a eigval [-2. -4.]
a eigvec
 [[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

[28]:

(0.0, 3.0)

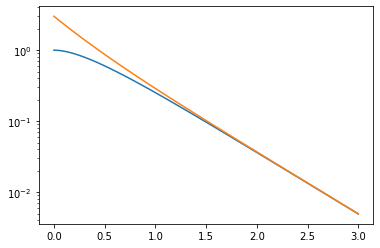
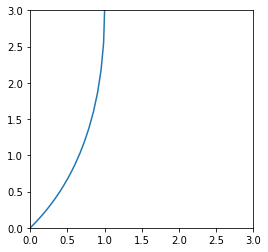
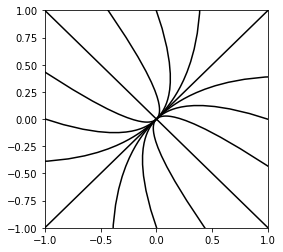
相図

[3]:

#### Phase Diagram


import matplotlib.pyplot as plt
import numpy as np
import scipy.linalg

a = np.array([[-3.,  1.], [ 1., -3.]])
print('a = ',  a)
eigval, eigvec = np.linalg.eig(a)
print('a eigval', eigval)
print('a eigvec\n', eigvec)

n = 16
x_0s = []
for i in range(n):
    x_0s.append(np.array([np.cos(2 * np.pi * i / n), np.sin(2 * np.pi * i / n)]))

fig, ax = plt.subplots(figsize=(4, 4))
ts = np.linspace(-1, 3)
for x_0 in x_0s:
    xs = []
    for t in ts:
        eta = scipy.linalg.expm(t * a)
        x = np.matmul(eta, x_0)
        xs.append(x)
    xs = np.array(xs)
    ax.plot(xs[:, 0], xs[:, 1], c='k')
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)

a =  [[-3.  1.]
 [ 1. -3.]]
a eigval [-2. -4.]
a eigvec
 [[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

[3]:

(-1.0, 1.0)

課題