| ◀ Previous | TOC | Next ▶ |
6. 極大極小(最適化)
6.1 scipy.optimize
例題 1
次の関数の極大値あるいは極小値を与える \(x\), およびその極大値あるいは極小値を求めよ.
\[y = x^2\]
例題 1 解答例
[2]:
import scipy.optimize
def func(x):
return x**2
x_0 = 2
res = scipy.optimize.minimize(func, x_0)
print('#### scipy.optimize.minimize default method')
print('The default method, described in the scipy documentation, is chosen as follows.')
print('"If ("method" is) not given, chosen to be one of BFGS, L-BFGS-B, SLSQP, depending if the problem has constraints or bounds.""')
print()
print(res)
print()
print()
res_nm = scipy.optimize.minimize(func, x_0, method='Nelder-Mead')
print('#### scipy.optimize.minimize Nelder-Mead method')
print(res_nm)
#### scipy.optimize.minimize default method
The default method, described in the scipy documentation, is chosen as follows.
"If ("method" is) not given, chosen to be one of BFGS, L-BFGS-B, SLSQP, depending if the problem has constraints or bounds.""
fun: 3.5662963072207506e-16
hess_inv: array([[0.5]])
jac: array([-2.2868119e-08])
message: 'Optimization terminated successfully.'
nfev: 9
nit: 2
njev: 3
status: 0
success: True
x: array([-1.88846401e-08])
#### scipy.optimize.minimize Nelder-Mead method
final_simplex: (array([[-1.77635684e-15],
[ 9.76562500e-05]]), array([3.15544362e-30, 9.53674316e-09]))
fun: 3.1554436208840472e-30
message: 'Optimization terminated successfully.'
nfev: 36
nit: 18
status: 0
success: True
x: array([-1.77635684e-15])
極値を与えるのは \(x=0\), その時の極小値は \(y=0\).
例題 1 コメント
Nelder-Mead 法が常に精度がいいわけではない.
方法(method=’’)の選択は問題の性質による.
例えば, Nelder-Mead は, 滑らかでない関数にも使える.
初期値をどのように与えるかが重要
scipy.optimize.minimize の詳細は https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html
scipy.optimize.minimize の default の method は変る可能性あり.
数年前には ‘Nelder-Mead’ が default だったと記憶する.
6.2 最適化とグラフ
例題 2
次の関数の極大値あるいは極小値を与える \(x\) を求めよ.
\[y = x^3 - 2 x^2 + x\]
例題 2 トライアル
[3]:
import scipy.optimize
def func3o(x):
return x**3 - 2 * x**2 + x
def neg_func3o(x):
return - (x**3 - 2 * x**2 + x)
x_0 = 0 # 初期値, 非線形最適化の場合, 初期値を設定する. 初期値依存性に注意.
res_local_min = scipy.optimize.minimize(func3o, x_0)
res_local_max = scipy.optimize.minimize(neg_func3o, x_0)
print('#### Local minimum')
print(res_local_min)
print()
print('#### Local maximum')
print(res_local_max)
#### Local minimum
fun: -4.58496271134698e+25
hess_inv: array([[1]])
jac: array([0.])
message: 'Optimization terminated successfully.'
nfev: 48
nit: 1
njev: 16
status: 0
success: True
x: array([-3.5791393e+08])
#### Local maximum
fun: -0.14814814814814808
hess_inv: array([[0.49994707]])
jac: array([-1.86264515e-09])
message: 'Optimization terminated successfully.'
nfev: 15
nit: 3
njev: 5
status: 0
success: True
x: array([0.33333332])
例題 2 トライアル, コメント
上記の結果はおかしい.
初期値を x_0 = 0.5 に変えてみると
[4]:
import scipy.optimize
def func3o(x):
return x**3 - 2 * x**2 + x
def neg_func3o(x):
return - (x**3 - 2 * x**2 + x)
x_0 = 0.5 # 初期値, 非線形最適化の場合, 初期値を設定する. 初期値依存性に注意.
res_local_min = scipy.optimize.minimize(func3o, x_0)
res_local_max = scipy.optimize.minimize(neg_func3o, x_0)
print('#### Local minimum')
print(res_local_min)
print()
print('#### Local maximum')
print(res_local_max)
#### Local minimum
fun: 0.0
hess_inv: array([[0.49944156]])
jac: array([1.49011612e-08])
message: 'Optimization terminated successfully.'
nfev: 27
nit: 5
njev: 9
status: 0
success: True
x: array([0.99999999])
#### Local maximum
fun: -0.14814814814797947
hess_inv: array([[0.50198089]])
jac: array([8.36327672e-07])
message: 'Optimization terminated successfully.'
nfev: 18
nit: 5
njev: 6
status: 0
success: True
x: array([0.33333374])
例題 2 解答例
\(x=1\) が極小値を与え, \(x=1/3\) が極大値を与える.
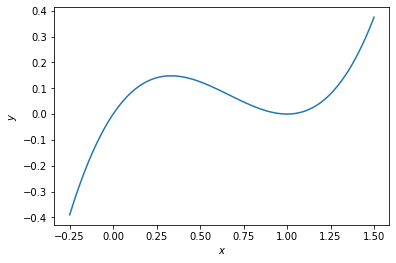
例題 2 グラフ
エンジニアならグラフで確認する.
というか, 描けるなら最初にグラフを描く.
多次元の場合, グラフが描けない場合も多い.
要は結果をチェックする工夫.
[41]:
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
fig, ax = plt.subplots()
x = np.linspace(-.25, 1.5, 200)
y = func3o(x)
ax.plot(x, y)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
[41]:
Text(0, 0.5, '$y$')
演習問題 1
次の関数のグラフを描き, その極大値, 極小値, および極大値, 極小値を与える \(x\) の値を求めよ.
\[x^4 + 4 x^3 + 4 x^2 - x - 1\]
演習問題 2
次の \(z\) の極小値を与える \([x, y]\) を求めよ.
ヒント: \(x\), \(y\) を配列として表す. 例えば
x = np.array([1, 1])
とおき, \(x=\)x[0], \(y=\)x[1] とする.
\[z = x^2 + y^2 + 2xy\]
| ◀ Previous | TOC | Next ▶ |