TOC

\(2 \times 2\) 行列は何をやっているのか

この章の目的

線形代数をより深く理解するために, 実 \(2 \times 2\) 行列が図形にどのように作用をするのかを調べる.

固有値がすべて実数で行列が対角化できる場合

対角化できる行列の作用

命題 2.1 対角化できる行列の作用

実 \(2 \times 2\) 行列が対角化できて固有値がすべて実数の場合, 行列は, 図形 (ベクトル)を固有ベクトルの方向に（その固有ベクトルに対応する）固有値倍する.

対角行列

まずは対角行列から始める.

例題 2.1

の固有値と固有ベクトルを求めよ.

(10)\[\begin{split}\begin{split} A = \begin{bmatrix}\begin{array}{lr} 3 & 0 \\ 0 & 2 \end{array}\end{bmatrix} \end{split}\end{split}\]

解答例題 2.1 \(A\) はすでに対角行列なので, 特に変換などの操作は不要である. \(A\) の固有値はその対角成分 \(\lambda_1 = 3\) , \(\lambda_2 = 2\) , であり, これに対応する固有ベクトルはそれぞれ \(x\) 方向, \(y\) 方向のベクトルである. 基準化すると以下のとおりである.

\[\begin{split}\begin{split} \boldsymbol e_1 = \begin{bmatrix}\begin{array}{r} 1 \\ 0 \end{array}\end{bmatrix}, \quad \boldsymbol e_2 = \begin{bmatrix}\begin{array}{r} 0 \\ 1 \end{array}\end{bmatrix} \end{split}\end{split}\]

解答は以上として, 例えば, ベクトル \(\boldsymbol a = [2, 1]^\mathrm T\) に上記の行列 \(A\) を作用させると次のようになる.

\[\begin{split}\begin{split} \boldsymbol b = A \boldsymbol a = \begin{bmatrix} \begin{array}{lr} 3 & 0 \\ 0 & 2 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{r} 2 \\ 1 \end{array} \end{bmatrix} = \begin{bmatrix} \begin{array}{r} 6 \\ 2 \end{array} \end{bmatrix} \end{split}\end{split}\]

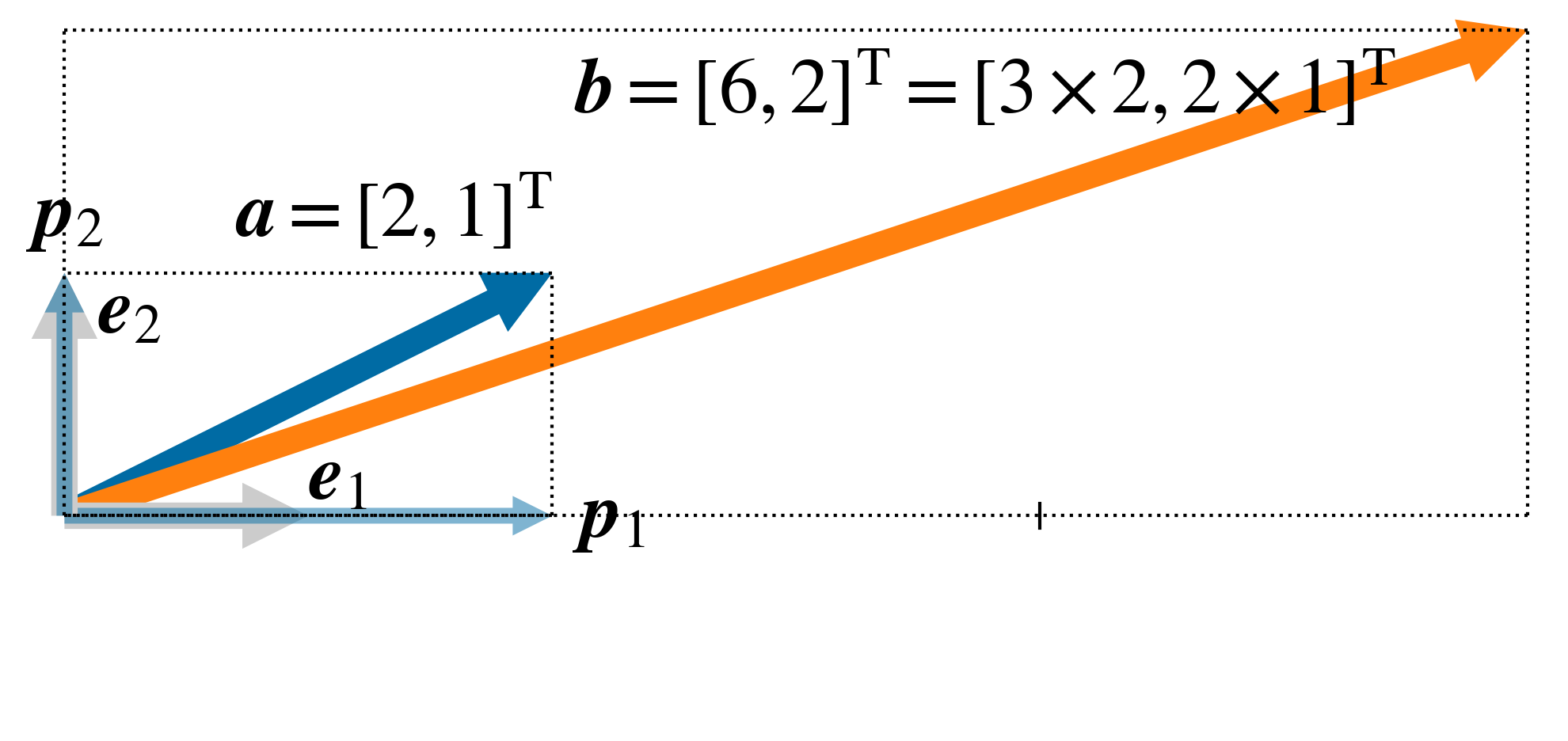
../_images/chap_2_effect_diagonal_matrix.png — 図 4 対角行列 \(A\) （式(10) ）のベクトル \(\boldsymbol a = \left[ 2, 1 \right]^\mathrm T\) への作用

この例では, ベクトル \(\boldsymbol b\) は, 固有ベクトル \(\boldsymbol e_1 = \left[1, 0\right]^\mathrm T\) の方向に固有値 \(\lambda_1 = 3\) 倍, 固有ベクトル \(\boldsymbol e_2 = \left[ 0, 1 \right]^\mathrm T\) の方向に固有値 \(\lambda_2 = 2\) 倍されている.

一般の対角化可能行列

例 2.2 対角化可能行列で固有値が2つの実数の場合

(11)\[\begin{split}\begin{split} B = \begin{bmatrix} \begin{array}{lr} -2 & 1 \\ 1 & -2 \end{array}\end{bmatrix} \end{split}\end{split}\]

この行列の固有値は \(\lambda_1 = -1\) , \(\lambda_2 = -3\) であり, ともに実数である. \(\lambda_1\) , \(\lambda_2\) に対応する固有ベクトル（基準化せず）は例えば \(\boldsymbol{p}_1 = [1, 1]^\mathrm{T}\) と \(\boldsymbol{p}_2 = [1, -1]^\mathrm{T}\) である. よって, 行列 \(B\) は \(P = \left[\boldsymbol p_1, \boldsymbol p_2\right]^\mathrm{T}\) を使って対角化できる.

\[\begin{split}\begin{aligned} J_B & = P^{-1}B P = \begin{bmatrix} \begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} -2 & 1 \\ 1 & -2 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} 1/2 & 1/2 \\ 1/2 & -1/2 \end{array} \end{bmatrix} \\ & = \begin{bmatrix} \begin{array}{rr} -1 & 0 \\ 0 & -3 \end{array} \end{bmatrix}\end{aligned}\end{split}\]

例えば, ベクトル \(\boldsymbol a = \left[3, 0\right]^\mathbb T\) に \(B\) が作用する場合を考えよう. \(\boldsymbol b = B \boldsymbol a\) とする. 行列 \(B\) の作用を固有ベクトルの基底で考える. 基底変換の概念を図示すると次の図 5 のようになる. すなわち, ベクトル \(\boldsymbol{a}\) に行列 \(B\) を作用させることは, ベクトル \(\boldsymbol{a}\) に, \(P^{-1}\) , \(J_B\) , \(P\) を順次作用させることと同じであり, \(B \boldsymbol a = P J_B P^{-1} \boldsymbol a\) と書ける. ここで, \(\boldsymbol{\xi}_{\boldsymbol{a}} = P^{-1} \boldsymbol{a}\) は, ベクトル \(a\) を元の基底（座標系）から固有ベクトルの基底に写したものであり, その \(\boldsymbol{\xi}_{\boldsymbol{a}}\) に固有ベクトル基底でのこの行列の作用を表す対角行列 \(J_B\) を作用させる, すなわち, 固有ベクトルの座標でそれぞれの成分を対応する固有値倍する作用となる. 最後に \(P\) は固有ベクトルの基底から元の基底に戻す操作を担っている.

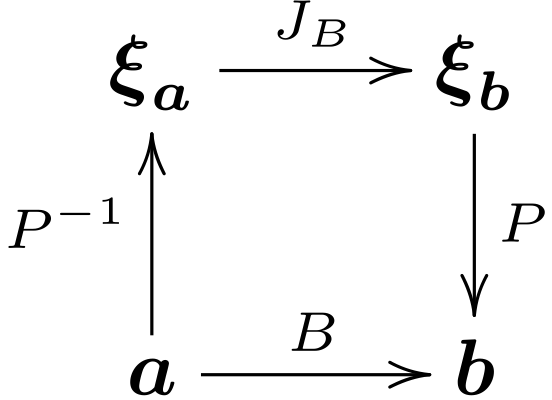
../_images/fig_basis_exchange.png — 図 5 基底変換

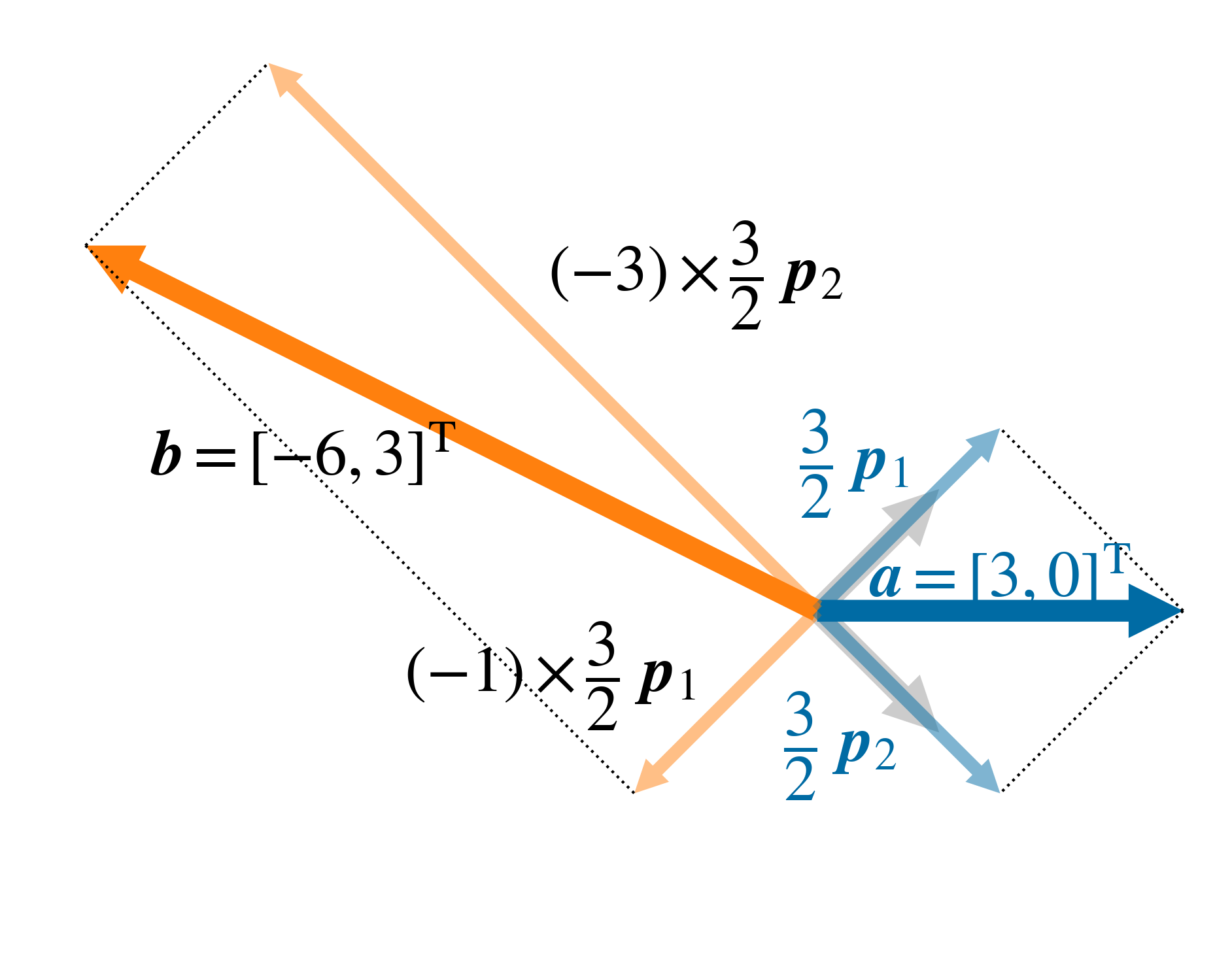
../_images/eigenvalues_times_eivenvector_directions.png — 図 6 対角化可能で固有値がすべて実数の行列 \(B\) （式(11) ）のベクトル \(\boldsymbol a = \left[1, 2 \right]^\mathrm T\) への作用

また, \(\boldsymbol a\) , \(\boldsymbol b = B \boldsymbol a\) と固有ベクトル, 固有値との関係を図示すると次の図 6 のようになる. 固有ベクトルの座標では, \(\boldsymbol a\) は次のように表される.

\[\begin{split}\begin{aligned} \boldsymbol \xi_{\boldsymbol a} = P^{-1} \boldsymbol a = \begin{bmatrix}\begin{array}{r} 3/2 \\ 3/2 \end{array}\end{bmatrix}\end{aligned}\end{split}\]

つまり, \(\boldsymbol a\) は固有ベクトル \(\boldsymbol p_1 = [1, 1]^\mathrm{T}\) と \(\boldsymbol p_2=[1, -1]^\mathrm{T}\) の次の線型結合となる.

\[\begin{aligned} \boldsymbol a = \boldsymbol{\xi}_{\boldsymbol a}[0] \boldsymbol p_1 + \boldsymbol{\xi}_{\boldsymbol{a}}[1] \boldsymbol p_2 = \frac{3}{2} p_1 + \frac{3}{2} \boldsymbol p_2\end{aligned}\]

これに対角行列 \(J_B\) が作用し, 固有ベクトル座標系での \(\boldsymbol b\) の座標 \(\boldsymbol \xi_{\boldsymbol b}\) を得る.

\[\begin{split}\begin{aligned} \boldsymbol \xi_{\boldsymbol b} = J_B \boldsymbol \xi_{\boldsymbol a} = \begin{bmatrix} \begin{array}{r} - 3/2 \\ -9/2 \end{array} \end{bmatrix}\end{aligned}\end{split}\]

\(J_B\) が作用することは, \(\boldsymbol \xi_{\boldsymbol a}\) の第1成分を \(\lambda_1\) 倍, 第2成分を \(\lambda_2\) 倍すること, すなわち, 固有ベクトルの方向に固有値倍する操作に他ならない. 元の座標系に戻すと

\[\begin{split}\begin{aligned} \boldsymbol b = P \boldsymbol \xi_{\boldsymbol b} = \begin{bmatrix} \begin{array}{r} -6 \\ 3 \end{array} \end{bmatrix}\end{aligned}\end{split}\]

となる. 以上, \(P\) と \(P^{-1}\) は基底変換（座標変換）を行っており, \(J_B\) が固有ベクトルの方向への変形という役割をになっている. この合成として, 固有ベクトルの方向に（対応する）固有値倍, という結果が得られるのである.

固有値が全て実数だが縮退している場合

縮退行列と Jordan 細胞

\(2 \times 2\) 行列の固有値が縮退している場合, 適当な基底変換 \(P\) , \(P^{-1}\) により次のような2次の Jordan 細胞 \(J_2\) の形になる. 2次以上の場合の Jordan 細胞については線形代数の教科書を参照するか, 検索するかしてほしい. Jordan 細胞を対角に並べた形の行列をJordan 標準形というのだった. また, 対角行列は1次の Jordan 細胞を対角に並べたものなので, Jordan 標準形の特別な場合である.

(12)\[\begin{split}\begin{split} J_2 = \begin{bmatrix} \begin{array}{rr} \lambda & 1 \\ 0 & \lambda \end{array} \end{bmatrix} \end{split}\end{split}\]

まずは, 行列 \(J_2\) がベクトルにどのように作用するかについて見る.

2次の Jordan 細胞

例 2.3 2 次の Jordan 細胞

(13)\[\begin{split}\begin{split} C = \begin{bmatrix}\begin{array}{rr} 2 & 1 \\ 0 & 2 \end{array}\end{bmatrix} \end{split}\end{split}\]

この \(C\) は, 式 (12) の \(J_2\) で \(\lambda = 2\) とおいた行列である. \(C\) がベクトルに作用すると, \(x\) 軸, \(y\) 軸の方向にそれぞれ 2 倍して, さらに \(x\) 軸の計算結果に元の \(y\) 軸の値を加えることになる. 図に示すと図 7 のようになる.

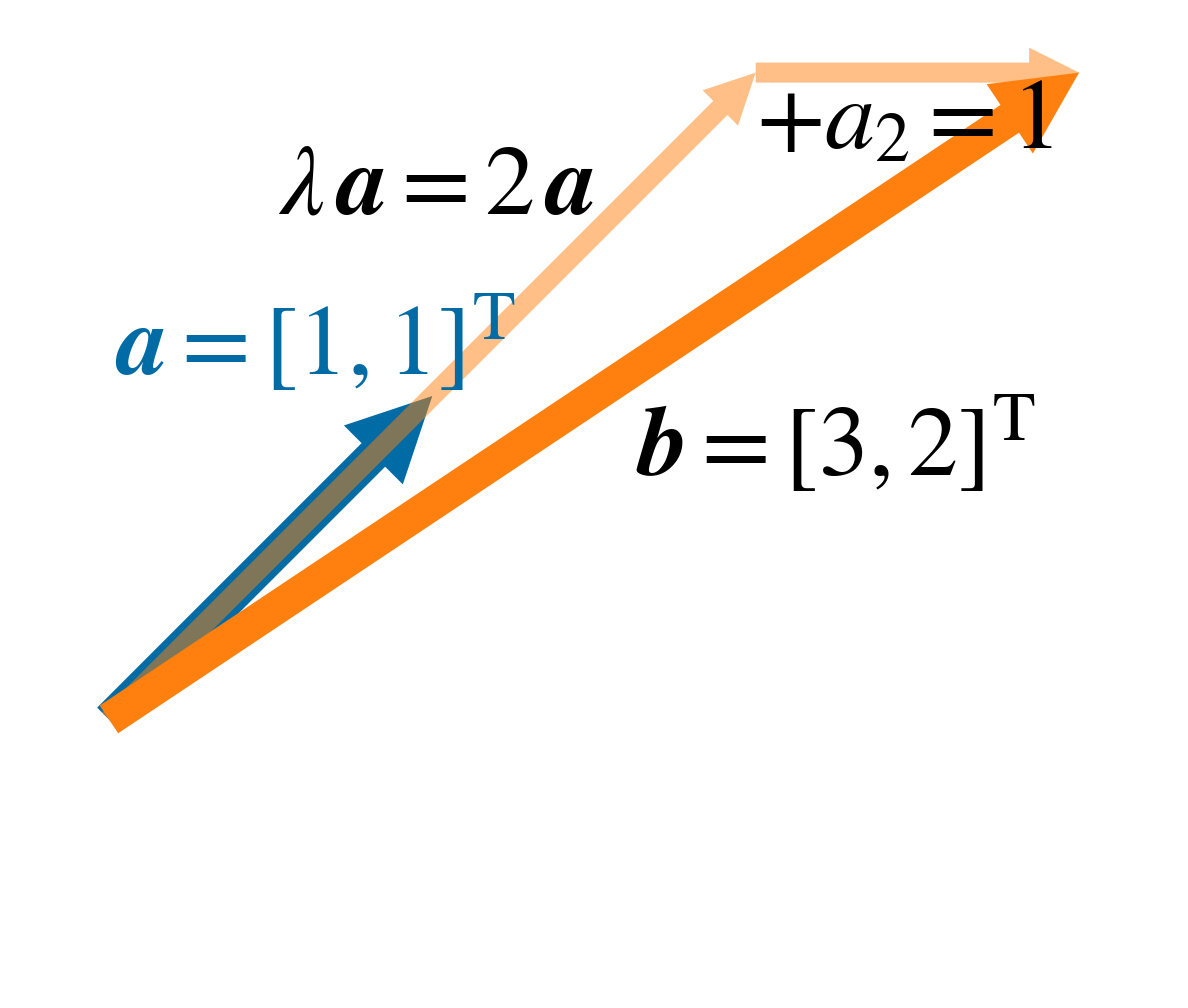
図 7 2次の Jordan 細胞 \(C\) （式(13) ）のベクトル \(\boldsymbol a = \left[1, 1\right]^\mathrm T\) への作用

参考までに, この行列の固有方程式は次のとおりで, 固有値は \(\lambda = 2\) （重解）.

\[\begin{split} \det \left( \lambda E - A \right) = (\lambda - 2) (\lambda - 2) = 0 \end{split}\]

固有, 広義固有ベクトルはそれぞれ \(\boldsymbol p_1 = \left[1, 0\right]^\mathrm T\) , \(\boldsymbol p^\prime_2 = \left[0, 1 \right]^\mathrm T\) である.

例 2.4

次の行列 \(D\) を考える.

(14)\[\begin{split}\begin{split} D = \begin{bmatrix} \begin{array}{rr} 3 & -1 \\ 1 & 1 \end{array} \end{bmatrix} \end{split}\end{split}\]

固有値は \(\lambda = 2\) （重解）. 固有ベクトルは \(\boldsymbol{p}_1 = \left[ 1, 1 \right]^{\mathrm{T}}\) , 広義固有ベクトルは \(\boldsymbol{p}_2 = \left[ 1/2, -1/2 \right]^{\mathrm{T}}\) よって, \(P = \left[ \boldsymbol{p}_1, \boldsymbol{p}_2\right]\) を使って標準化して

\[\begin{split}\begin{split} J & = P^{-1} D P = \begin{bmatrix} \begin{array}{rr} 1/2 & 1/2 \\ 1 & -1 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} 3 & -1 \\ 1 & 1 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} 1 & 1/2 \\ 1 & -1/2 \end{array} \end{bmatrix} %\\ & = \begin{bmatrix} \begin{array}{rr} 2 & 1 \\ 0 & 2 \end{array} \end{bmatrix} \end{split}\end{split}\]

\(\boldsymbol a = \left[1, 0\right]^{\mathrm{T}}\) にこの行列 \(D\) を作用させた場合を考える.

次式に計算過程を, 図 8 にこの \(\boldsymbol a\) , \(\boldsymbol b\) , \(\boldsymbol p_1\) , \(\boldsymbol p_2^\prime\) の関係を示す. \(\boldsymbol b\) はベクトル \(\boldsymbol{a}\) に固有値 \(\lambda=2\) を掛けたものに, \((P^{-1}\boldsymbol a)_2 \times \boldsymbol p_1\) を足したものになっている.

\[\begin{split}\begin{aligned} \boldsymbol{b} & = P D P^{-1} a = \begin{bmatrix} \begin{array}{rr} 1 & 1/2 \\ 1 & -1/2 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} 2 & 1 \\ 0 & 2 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} 1/2 & 1/2 \\ 1 & -1 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{r} 1 \\ 0 \end{array} \end{bmatrix} \\ & = \begin{bmatrix} \begin{array}{rr} 1 & 1/2 \\ 1 & -1/2 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} 2 & 1 \\ 0 & 2 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{r} 1/2 \\ 1 \end{array} \end{bmatrix} %\\ & = \begin{bmatrix} \begin{array}{rr} 1 & 1/2 \\ 1 & -1/2 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{r} 2 \\ 2 \end{array} \end{bmatrix} %\\ & = \begin{bmatrix} \begin{array}{r} 3 \\ 1 \end{array} \end{bmatrix}\end{aligned}\end{split}\]

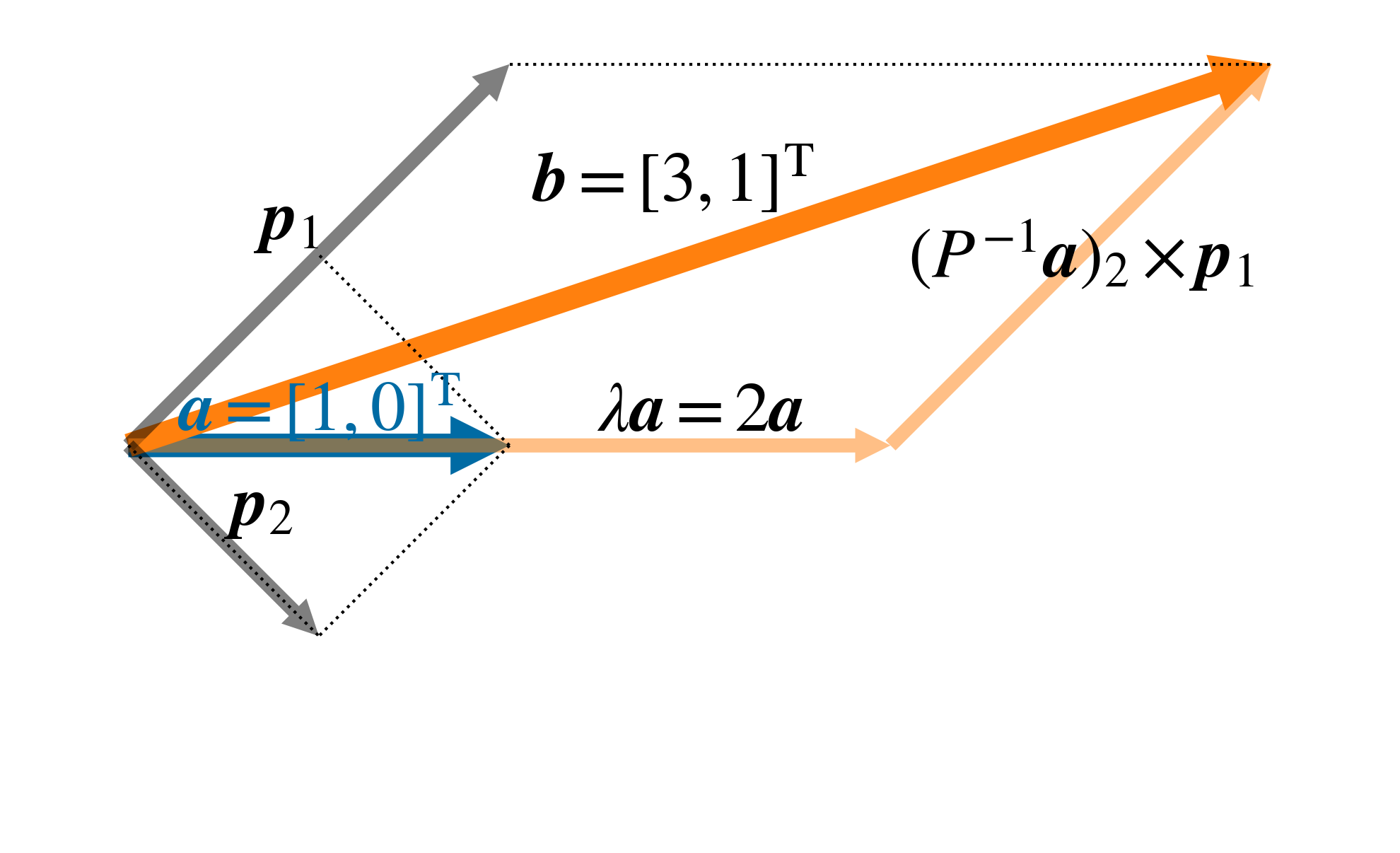
../_images/effect_degenerated_matrix.png — 図 8 退化行列 \(D\) (14) のベクトル \(\boldsymbol a = \left[1, 0\right]^\mathrm{T}\) への作用

固有値が共役複素数を含む場合（回転・回転と拡大）

基礎知識

命題 2.5

実行列が虚数の固有値をもつ場合, その共役複素数も固有値となる.

命題 2.6

実行列が共役複素数の固有値をもつ場合, 行列は図形を回転する作用を含む.

命題 2.7 Euler の公式, Euler's formula

(15)\[\begin{split} e^{i\theta} = \cos \theta + i \sin \theta \end{split}\]

回転を表す行列

原点まわりの角度 \(\theta\) だけの回転を表す行列は,

(16)\[\begin{split}\begin{split} R = \begin{bmatrix} \begin{array}{rr} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array} \end{bmatrix} \end{split}\end{split}\]

行列 \(R\) の固有方程式は

\[\begin{split} \det \left( R - \lambda E \right) = \lambda^2 - 2 \cos \theta \lambda + 1 = 0 \end{split}\]

これより,

\[\begin{split} \lambda_1, \lambda_2 = \cos \theta \pm i \, \sin \theta \end{split}\]

となり, 固有値が互いに共役複素数であることが分かる. また, Euler の公式(15) より

\[\begin{split} \lambda_1, \lambda_2 = e^{\pm i\theta} \end{split}\]

例 2.8

\[\begin{split}\begin{split} F = \begin{bmatrix} \begin{array}{rr} \frac{1}{2} & - \frac{\sqrt 3}{2} \\ \frac{\sqrt 3}{2} & \frac{1}{2} \end{array} \end{bmatrix} \end{split}\end{split}\]

この行列の固有方程式は

\[\begin{split} \det \left(F - \lambda E \right) = \lambda^2 - \lambda + 1 = 0 \end{split}\]

よって, 固有値は

\[\begin{split}\begin{aligned} \lambda_1 & = \frac{1 + \sqrt 3 i}{2} = \cos \frac{\pi}{3} + i\sin \frac{\pi}{3} = e^{i \frac{\pi}{3}}, \\ \lambda_2 & = \frac{1 - \sqrt 3 i}{2} = \cos \frac{\pi}{3} - i\sin \frac{\pi}{3} = e^{-i \frac{\pi}{3}}\end{aligned}\end{split}\]

で, この行列 \(F\) は原点まわりの角度 \(\pi/3\) あるいは \(-\pi/3\) の回転を表すことが分かる. 実際

\[\begin{split}\begin{split} F = \begin{bmatrix} \begin{array}{rr} \cos \pi/3 & - \sin \pi /3 \\ \sin \pi/3 & \cos \pi /3 \end{array} \end{bmatrix} \end{split}\end{split}\]

である. 固有値のみでは, 回転角が \(+\pi/3\) か \(- \pi/3\) かは分からない.

回転と拡大・縮小を表す行列

次の形の行列は, 回転と拡大・縮小を行う

\[\begin{split}\begin{split} G = \begin{bmatrix} \begin{array}{rr} a & -b \\ b & a \end{array} \end{bmatrix}, \quad a, b \in \mathbb R \end{split}\end{split}\]

なぜなら

(17)\[\begin{split}\begin{split} G &= \sqrt{a^2 + b^2} \begin{bmatrix} \begin{array}{rr} \dfrac{a}{\sqrt{a^2 + b^2}} & - \dfrac{b}{\sqrt{a^2 + b^2}} \\ \dfrac{b}{\sqrt{a^2 + b^2}} & \dfrac{a}{\sqrt{a^2 + b^2}} \end{array} \end{bmatrix} \\ & = \sqrt{a^2 + b^2} \begin{bmatrix} \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \end{bmatrix} \end{split}\end{split}\]

ここで \(\cos \theta= \frac{a}{\sqrt{a^2 + b^2}}\) , \(\sin \theta = \frac{b}{\sqrt{a^2 + b^2}}\)

例 2.9

\[\begin{split}\begin{split} H = \begin{bmatrix}\begin{array}{rr} 2 & - 4 \\ 4 & 2 \end{array}\end{bmatrix} \end{split}\end{split}\]

固有値は \(\lambda_1 = 2 + 4i\) , \(\lambda_2 = 2 - 4 i\) . 上記の式(17) に倣って書き換えると

\[\begin{split}\begin{split} H = 2\sqrt 5 \begin{bmatrix}\begin{array}{rr} \frac{1}{\sqrt 5} & - \frac{2}{\sqrt 5} \\ \frac{2}{\sqrt 5} & \frac{1}{\sqrt 5} \end{array}\end{bmatrix} \end{split}\end{split}\]

\(H\) は \(\cos \theta = 1/ \sqrt 5\) , \(\sin \theta = 2 / \sqrt 5\) となる角度 \(\theta\) だけ回転して大きさを \(2\sqrt 5\) 倍に拡大する作用をもつ.

固有値が共役複素数を含む場合（一般の場合・極分解）

半正定値行列の平方根\(^*\)

固有値に共役複素数を含む実行列が図形に作用するとき, 回転の作用を含む. このとき, もとの行列は, 回転行列と半正定値行列の積で表すことができる. このような, 回転行列と半正定値行列の積への分解は, 極分解と言われるものの一部である. 極分解は入門レベルの教科書には扱われない場合が多いので, ここで解説しておく.

極分解について学ぶ前に, 行列の平方根について知る必要がある. この項では, 半正定値行列の平方根と主平方根について学ぶ. 半正定値（実）行列とは対称行列でその固有値がすべて非負のもののことであった. 実対称行列は必ず対角化できるので, 半正定値行列 \(A\) は必ず対角化できる. \(A\) が固有ベクトルを並べた行列 \(P\) によって \(J = P^{-1} A P\) と対角化できるとしよう. このとき, \(A = P J P^{-1}\) だが, \(J\) は対角行列でその成分は仮定から非負なので, \(K^2=J\) となるような行列 \(K\) を考えることができる. 具体的に \(2 \times 2\) 行列で考えると \(a\ge 0\) , \(b\ge 0\) として,

\[\begin{split}\begin{split} J = \begin{bmatrix}\begin{array}{rr} a & 0 \\ 0 & b \end{array} \end{bmatrix} , \quad K = \begin{bmatrix} \begin{array}{rr} \sqrt a & 0 \\ 0 & \sqrt b \end{array} \end{bmatrix} \end{split}\end{split}\]

が \(K^2 = J\) をみたしている. ここで \(B = P K P^{-1}\) なる行列を考えよう. 簡単な計算で

\[\begin{split}\begin{aligned} B^2 &= \left(P K P^{-1} \right)^2 %\\ & = \big(P K \underbrace{P^{-1} \big)\big(P}_{=E} K P^{-1} \big) \\ & = P K^2 P^{-1} = P J P^{-1} = A\end{aligned}\end{split}\]

すなわち \(B = P K P^{-1}\) が \(A\) の平方根であることが分かる. さて, あきらかに, 次の行列

\[\begin{split}\begin{split} K_1=\begin{bmatrix} \begin{array}{rr} \sqrt a & 0 \\ 0 & -\sqrt b \end{array} \end{bmatrix} , \quad K_2=\begin{bmatrix} \begin{array}{rr} - \sqrt a & 0 \\ 0 & \sqrt b \end{array} \end{bmatrix} , \quad K_3=\begin{bmatrix} \begin{array}{rr} - \sqrt a & 0 \\ 0 & -\sqrt b \end{array} \end{bmatrix} \end{split}\end{split}\]

も, \(K_i^2 = J\) \((i=1, 2, 3)\) を満たしている. 実数 \(a \ge 0\) の平方根が \(\pm \sqrt a\) と符号の不定性をもつのと同じである. 実数の場合に \(b^2=a \ge 0\) のうち, \(b \ge 0\) を満たすものを \(\sqrt a\) と記したのと同じように, 行列の平方根においても, 対角化行列の成分がすべて非負であるもの（上の例では \(B=PKP^{-1}\) ）を選び, 主平方根とよび, \(\sqrt A\) などと記す. 平方根のうち, 対角化行列の成分がすべて非負, すなわち固有値が全て非負のものはひとつしかないから, これは一意に定まる.

\(A=PK^2P^{-1}\) は, 対角行列 \(J=K^2\) の左右に \(P\) と \(P^{-1}\) を作用させたものだが, これが対称だった. このことから, その主平方根 \(B=PKP^{-1}\) も対角行列 \(K\) の左右に \(P\) と \(P^{-1}\) を作用させたものだから対称だと分かる. \(B\) は固有値がすべて非負の対称行列なので半正定値である. 以上のことを定理にまとめる.

定理 2.10

\(A\) を半正定値行列とすると, \(B^2 = A\) となる半正定値行列 \(B\) が存在し一意に定まる. このような行列 \(B\) を \(A\) の主平方根（principal square root）とよび, \(\sqrt A\) などと表す.

系 2.11

成分が非負（\(j_i \ge 0\) , \(i=1, \dotsc, n\) ）の対角行列

\[\begin{split}\begin{split} J = \begin{bmatrix} \begin{array}{rrrr} j_1 &&& \\ & j_2 & & \\ && \ddots & \\ &&& j_n \end{array} \end{bmatrix} \end{split}\end{split}\]

の主平方根は

\[\begin{split}\sqrt J = \begin{bmatrix} \begin{array}{rrrr} \sqrt {j_1} &&& \\ & \sqrt {j_2} & & \\ && \ddots & \\ &&& \sqrt {j_n} \end{array} \end{bmatrix}\end{split}\]

である.
半正定値行列 \(A\) が \(A= P J P^{-1}\) と対角化できるとき, その主平方根は \(P \sqrt J P^{-1}\) で与えられる.

備考 2.12

表記 \(\sqrt A\) は常に主平方根を表すわけでもないようである. 文脈に注意する必要がある.

例題 2.2

\[\begin{split}\begin{split} A = \begin{bmatrix} \begin{array}{r r} 19 & -15 \\ 10 & -6 \end{array} \end{bmatrix} \end{split}\end{split}\]

[examplep: square root matrix]

解答例題 2.2

\(A\) の固有値は \(\lambda_1 = 4\) , \(\lambda_2 = 9\) 対応する固有ベクトルは \(\boldsymbol p_1 = [1, 1]^\mathrm T\) , \(\boldsymbol p_2 = [3, 2]^\mathrm T\) , これより, \(P = \left[ \boldsymbol p_1, \boldsymbol p_2 \right]\) を使って

\[\begin{split}\begin{aligned} A & = P J P^{-1} \\ & = \begin{bmatrix} \begin{array}{rr} 1 & 3 \\ 1 & 2 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} 4 & 0 \\ 0 & 9 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} -2 & 3 \\ 1 & -1 \end{array} \end{bmatrix}\end{aligned}\end{split}\]

と表すことができる. \(A\) の主平方根 \(B\) はつぎのように計算される.

\[\begin{split}\begin{aligned} B & = P \sqrt J P^{-1} %\\ & = \begin{bmatrix} \begin{array}{rr} 1 & 3 \\ 1 & 2 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} 2 & 0 \\ 0 & 3 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} -2 & 3 \\ 1 & -1 \end{array} \end{bmatrix} \\ & = \begin{bmatrix} \begin{array}{rr} 5 & -3 \\ 2 & 0 \end{array} \end{bmatrix}\end{aligned}\end{split}\]

極分解\(^*\)

定理 2.13 極分解（右極分解）

直交行列 \(U\) と半正定値対称行列 \(S\) によって

\[A = US\]

と分解できる. この分解は一意である.

証明の前に補題をふたつ記しておく.

補題 2.14

任意の実行列 \(A\) について（正方行列以外でもよい）\(A^\mathrm T A\) は対称行列である.

Proof. （補題 2.14 ）

\[\begin{split} (A^\mathrm T A)^\mathrm T = A ^\mathrm T \left(A^\mathrm T \right)^\mathrm T = A^\mathrm T A. \end{split}\]

◻

補題 2.15

\(A^\mathrm T A\) は半正定値である.

Proof. （補題 2.15 ）任意の実ベクトル \(\boldsymbol x\) に対し

\[\begin{split} \boldsymbol x^\mathrm T A^\mathrm T A \boldsymbol x = (A \boldsymbol x)^\mathrm T (A \boldsymbol x) \ge 0. \end{split}\]

最後の不等号であるが, \(A \boldsymbol x\) は実ベクトルで, \((A \boldsymbol x)^\mathrm T (A \boldsymbol x)\) は, \(A \boldsymbol x\) の各要素を 2 乗したものの和なので, 非負である.　 ◻

極分解の証明の考え方は次のとおり. 行列 \(A\) が直交行列 \(U\) と半正定値行列 \(S\) によって \(A = US\) と分解できたとすると

\[\begin{split}\begin{aligned} A^\mathrm T A & = (US)^\mathrm T (US) = S^{\mathrm T} U^{\mathrm T} U S \\ & = S (U^\mathrm T U) S = S^2.\end{aligned}\end{split}\]

ここで, 直交行列の次の性質を使っている \(U^\mathrm T U = U^{-1} U = E\) . \(S\) は半正定値行列と仮定したので対称だから \(S^\mathrm T = S\) . さて, この \(S\) は \(A^\mathrm T A\) の平方根であるが, \(S\) は半正定値行列, という条件があるので, 主平方根として一意に定まる. では, 証明に移るが, ここでは簡単のため, 正則行列についてのみ証明を記す. 一般の場合は逆行列の存在が保証されないので, 少々面倒になる.

Proof. （定理 2.13 , \(A\) が正則行列の場合） \(A^\mathrm T A\) は, 補題 2.15 により半正定値行列となるので, その主平方根（principal square root）\(S = \sqrt{A^\mathrm T A}\) は半正定値行列として一意に定まる. \(A\) は正則と仮定したから \(A^\mathrm T A\) も正則, したがって \(S\) も正則. よって \(S^{-1}\) が存在する. \(U = A S^{-1}\) とおく. この \(U\) については,

\[U^\mathrm T U= (A S^{-1})^\mathrm T A S^{-1} = S^{-1} A^\mathrm T A S^{-1} = S^{-1} S^2 S^{-1} = E\]

となり, \(U\) が直交行列であることが分かる. ◻

固有値が共役複素数の正則行列・回転と半正定値行列への分解\(^*\)

定理 2.16

\(2 \times 2\) 実正方行列 \(A\) が, 共役複素数固有値をもつ場合, その行列の作用は, 回転を表す行列 \(R\) と半正定値行列 \(S\) に \(A = RS\) と分解できる.

Proof. 任意の実行列は, 直交行列と半正定値行列の積に分解できる（極分解）が, \(2 \times 2\) 実正方行列が共役複素数固有値をもつ場合, この行列には回転の作用が含まれる. \(2 \times 2\) 直交行列は, 原点まわりの回転か, 原点を通る直線に対する線対称移動を表すが, 元の行列の固有値が共役複素数の場合, 直交行列は回転を表す行列になる. ◻

備考 2.17

\(2 \times 2\) 直交行列の固有値が共役複素数の場合, その直交行列が回転行列であることの証明は省略する. 気になる人は, 回転の行列, 原点を通る直線に対する線対称移動の行列を作って, 固有値を計算してみるとよい.

例題 2.3

\(R\) と半正定値行列 \(S\) の積に \(M=RS\) と極分解せよ.

\[\begin{split}\begin{split} M = \begin{bmatrix} \begin{array}{rr} 0.9 & - 0.5 \\ 1.3 & 1.5 \end{array} \end{bmatrix} \end{split}\end{split}\]

解答例題 2.3

\[\begin{split}\begin{split} M^\mathrm T M = \begin{bmatrix} 2.5 & 1.5 \\ 1.5 & 2.5 \end{bmatrix} \end{split}\end{split}\]

\(M^\mathrm T M\) は実対称行列なので対角化できる. \(M^\mathrm T M\) の固有値は \(\lambda = 4, 1\) で, 対応する固有ベクトルはそれぞれ例えば, \(\boldsymbol p_1 = \left[1 , 1\right]^\mathrm T\) , \(\boldsymbol p_2 = \left[1 , -1 \right]^\mathrm T\) . これを並べた行列を \(P = \left[ \boldsymbol p_1, \boldsymbol p_2 \right]\) として

\[\begin{split}\begin{split} M^\mathrm T M = P J P^{-1}, \quad J = \begin{bmatrix}\begin{array}{rr} 4 & 0 \\ 0 & 1 \end{array}\end{bmatrix} \end{split}\end{split}\]

\(M^\mathrm T M\) の行列の平方根は, これより \(S=P \sqrt J P^{-1}\) だから

\[\begin{split}\begin{split} S &= \sqrt{M^\mathrm T M} = P \begin{bmatrix} \begin{array}{rr} 2 & 0 \\ 0 & 1 \end{array} \end{bmatrix} P^{-1} = \begin{bmatrix} \begin{array}{rr} 3/2 & 1/2 \\ 1/2 & 3/2 \end{array} \end{bmatrix} \\ U &= M S^{-1} = \begin{bmatrix} \begin{array}{rr} -0.9 & 0.5 \\ - 1.3 & 1.5 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} 3/4 & -1/4 \\ - 1/4 & 3/4 \end{array} \end{bmatrix} = \begin{bmatrix} \begin{array}{rr} 4/5 & -3/5 \\ 3/5 & 4/5 \end{array} \end{bmatrix} \end{split}\end{split}\]

これは \(\cos \theta = 4/5\) , \(\sin \theta = 3/5\) なる角度 \(\theta\) だけの回転を表す行列である. よって

\[\begin{split}\begin{split} M = U S = \begin{bmatrix} \begin{array}{rr} 4/5 & -3/5 \\ 3/5 & 4/5 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} 3/2 & 1/2 \\ 1/2 & 3/2 \end{array} \end{bmatrix} \end{split}\end{split}\]

と, 回転を表す行列 \(U\) と半正定値行列 \(S\) に分解できた.

備考 2.18

計算手順から, この分解は, \(S\) として \(\pm \sqrt J\) がとれることを除けば一意であるから, \(S\) が半正定値であるとの条件から \(S = \sqrt J\) と一意に定まる.

演習問題

問題 2.1

次の行列が図形に作用した時, (a) 各固有ベクトルの方向にそれぞれの固有ベクトル倍, (b) 回転, (c) 回転と拡大・縮小 (d) いずれでもない, のいずれの結果となるか示せ.

\[\begin{split}\begin{aligned} & A = \begin{bmatrix} \begin{array}{rr} a & 0 \\ 0 & b \end{array}\end{bmatrix}, \quad a \ne 0, \ b \ne 0, \\ & B = \begin{bmatrix} \begin{array}{rr} 2 & 1 \\ -1 & 2 \end{array} \end{bmatrix}, \quad C = \begin{bmatrix} \begin{array}{rr} 4 & -1 \\ -2 & 5 \end{array} \end{bmatrix}, \quad \\ & D = \begin{bmatrix} \begin{array}{rr} 4 & 1 \\ -2 & 5 \end{array} \end{bmatrix}, \quad G = \begin{bmatrix} \begin{array}{rr} 3 & 1 \\ 0 & 3 \end{array} \end{bmatrix}\end{aligned}\end{split}\]

問題 2.2

次の行列 \(A\) を考える.

\[\begin{split}\begin{split} A = \begin{bmatrix} \begin{array}{rr} \frac{11}{4} & \frac{\sqrt 3}{4} \\ \frac{\sqrt 3}{4} & \frac{9}{4} \end{array} \end{bmatrix} \end{split}\end{split}\]

この行列 \(A\) は対称行列であるから, 対角化できる. この行列の固有値は \(\lambda_1 = 3\) , \(\lambda_2 = 2\) で, それぞれに対応する固有ベクトルは (正規化して) 次の通りである.

\[\begin{split} \boldsymbol p_1 = \left[\sqrt 3/{2}, {1}/{2} \right], \quad \boldsymbol p_2 = \left[- {1/2}, \sqrt 3/2 \right] \end{split}\]

次の問に答えよ.

対角化行列 \(J\) を求めよ.
固有ベクトルの座標で \(\boldsymbol a = [1, 1]^{\mathrm T}\) を表せ. すなわち, 次を満たすような \(\boldsymbol \alpha = [\alpha_1, \alpha_2 ]^{\mathrm T}\) を求めよ.

\[\boldsymbol a = \alpha_1 \boldsymbol p_1 + \alpha_2 \boldsymbol p_2\]

対角化行列を \(\boldsymbol \alpha\) に作用させた結果のベクトル \(\boldsymbol \beta\) を求めよ.
\([\boldsymbol p_1, \boldsymbol p_2] \boldsymbol \beta\) の結果を求めよ. ただし, \([\boldsymbol p_1, \boldsymbol p_2]\) は固有ベクトルを並べて作られる行列とする.
\(A\boldsymbol a\) が 4. の結果と一致することを確かめよ.

問題 2.3

次の行列の主平方根を求めよ.

\[\begin{split}A = \begin{bmatrix} \begin{array}{rr} -1 & 5 \\ -10 & 14 \end{array} \end{bmatrix} , \quad B = \begin{bmatrix} \begin{array}{rr} -8 & 18 \\ -6 & 13 \end{array} \end{bmatrix}\end{split}\]

問題 2.4

つぎの行列 \(C\) は回転と拡大 (縮小) を表す行列である.

回転角の \(\sin\) と \(\cos\) を求めよ. 半時計回りに回転するとする.
図形の拡大を拡大倍数 (縮小の場合はこの数が 1 未満) を求めよ.

\[\begin{split}\begin{split} C = \begin{bmatrix} \begin{array}{rr} 3 & 4 \\ -4 & 3 \end{array} \end{bmatrix} \end{split}\end{split}\]

問題 2.5

次の行列を考える.

\[\begin{split}\begin{split} D = \begin{bmatrix} \begin{array}{rr} 4 & -1 \\ 4 & 8 \end{array} \end{bmatrix} , \quad P = \begin{bmatrix} \begin{array}{rr} 2 & -1 \\ -4 & 0 \end{array} \end{bmatrix} \end{split}\end{split}\]

\(P^{-1} D P\) を計算せよ.
\(D\) の固有値と固有ベクトルを求めよ (1 組だけで良い. ただし, 一般化固有ベクトルが分かる人はもう 1 組みとしてそれも求められればなおよい).

問題 2.6

次の行列を回転の行列と半正定値行列の積に右極分解せよ.

\[\begin{split}\begin{split} A = \begin{bmatrix} \begin{array}{rr} 5 & -2 \\ 10 & 11 \end{array} \end{bmatrix} \end{split}\end{split}\]

◀ Previous

TOC

Next ▶

微分積分・線形代数の次に学ぶ数学