TOC

極大点・極小点を求めるアルゴリズム

この章で学ぶこと

現在, 最適化で最もよく用いられているのは, おそらく, Newton 法と勾配降下法だろう. 前者は効率よく最適値を求めるのに適しており, 後者は 1 階微分のみを使うという計算負荷上の利点から機械学習で用いられる（実際には派生法である確率的勾配降下法がよく用いられる）.

最適化の難しさは, 過学習や, 初期値の設定方法, などアルゴリズムとは違ったところにあることが多いが, それでも, アルゴリズムを理解していれば, 問題に対してより適切な対処ができる可能性が高まる. そのような観点から, この章では, Newton 法と勾配降下法を学ぶ.

最適化のアルゴリズム（1変数）

Newton 法

Newton 法（Newton Raphson 法）は, 極小値を求めるというよりは, 方程式 $f (x) = 0$ の解を求める方法である. 極小値を求めるためには, 1 階微分のゼロ点 $d f / d x = 0$ つまり停留点を求める. 図 22 に $y = f (x) = 0$ の解を求める例を示す.

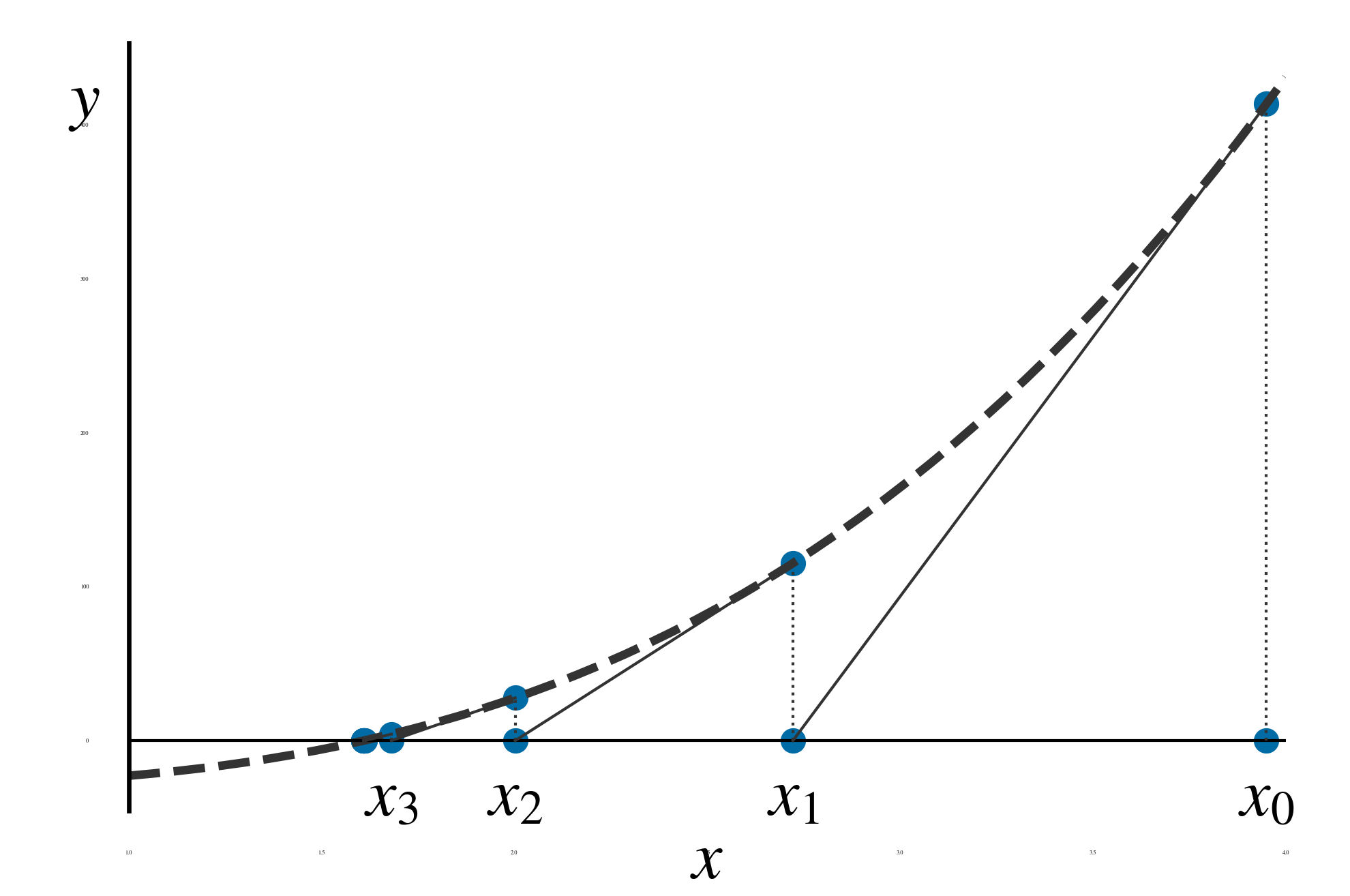
../_images/newton_solving_equation.png — 図 22 1 変数の場合の Newton 法による方程式 $y = f (x) = 0$ の解の求め方

まず, 適当な初期値 $x_{0}$ を決める. 次に, その初期値における関数の値 $f (x_{0})$ を求める. 点 $(x_{0}, f (x_{0}))$ から, 接線（傾き $f^{'} (x)$ ）を引く. 接線と $x$ 軸（ $y = 0$ ）との交点を求め, $x_{1}$ とする. 以下, $(x_{i}, f (x_{i}))$ から接線を引いて $x$ 軸との交点 $x_{i + 1}$ を求めることを繰り返す. $| f (x_{i + 1}) | < ε_{0}$ となったら, $x_{i + 1}$ を解の近似値として採用し, 計算を終える.

Newton 法で極大・極小点を求めるには, 停留点を求める. 求めた停留点が極大点か極小点かについては, 第 1 章に述べた方法で別に調べる必要がある. 図 23 に停留点を Newton 法で求めるときの $x$ の更新過程の例を示す. $f^{'} (x) = 0$ を解くことで, 関数 $f (x)$ の極小点が求まっている. 図 24 に, Newton 法で停留点を求めるアルゴリズムを示しておく.

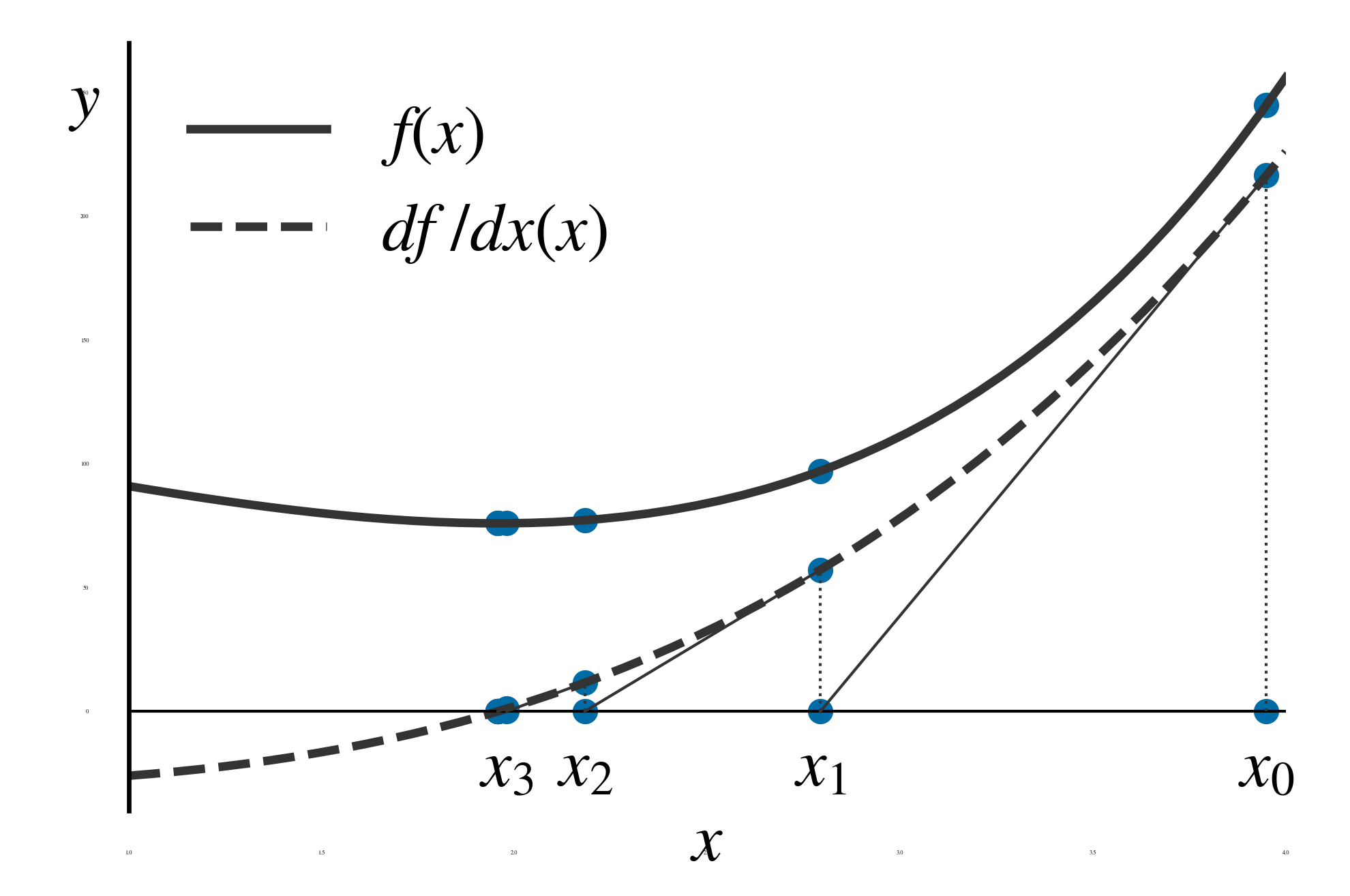
../_images/newton_solving_derivative_zero.png — 図 23 1 変数の場合の Newton 法による停留点の求め方の例, 実線 $f (x)$ , 破線 $f^{'} (x)$

../_images/fig_algorithm_newton_one.png — 図 24 Newton 法により停留点を求めるアルゴリズム

勾配降下法

勾配降下法では関数の勾配（が最大になる）方向に勾配に比例するだけ移動する. 関数の谷を降りていき, 谷底（極小点）に到達すれば, 勾配が 0 になるので, 移動が止まる. 計算には, 学習率（learning rate）と呼ばれるパラメーターを用いるが, この値により収束速度が大きく異なり, 場合によっては収束しないこともある. 図 25 に勾配降下法での極小点を求めるまでの $x_{i}$ の更新の様子の例を示す.

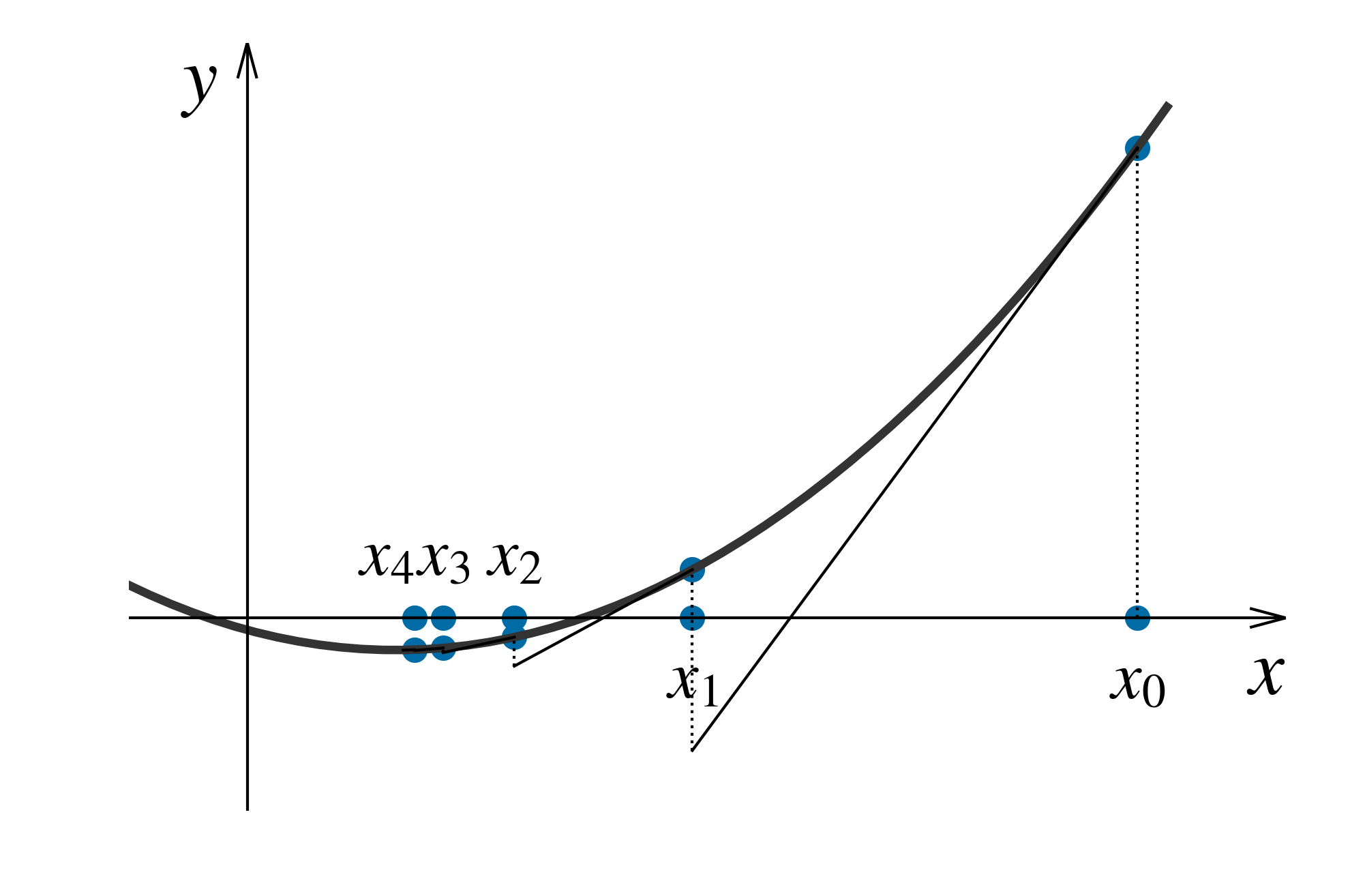
../_images/gradient_descent.png — 図 25 勾配降下法による極小点の求め方の例

図 26 に, 勾配降下法のアルゴリズムを示す.

../_images/fig_algorithm_GD_one.png — 図 26 勾配降下法のアルゴリズム

Newton 法と勾配降下法の比較

Newton 法では, $f^{'}$ の接線と $y = 0$ との交点を更新点として用いるが, 勾配降下法では, $f$ の接線方向に, その傾きに比例した分だけ $x$ を変化させる. Newton 法で停留点を求めるためには, アルゴリズムからも分かるように, $f^{'} (x_{i})$ と $f^{''} (x_{i})$ が必要である. 勾配降下法では, $f^{'} (x_{i})$ だけが必要である.

備考 4.1

アルゴリズムから分かるが, Newton 法は停留点に収束する. つまり極大値にも収束する. 勾配降下法は極小値のみに収束し, 極大値に収束することはない.

例題 4.1

$x_{0} = 2$ からの 1) Newton 法, 2) 勾配降下法で, ともに収束条件を $| f^{'} (x_{i}) | < ε_{0}$ , $ε = 1.0 \times 10^{- 4}$ として求めよ. ただし, 勾配降下法の学習率は $η = 0.1111$ とする.

\begin{array}{r} y = f (x) = x^{3} - 3 x \end{array}

この問題はできれば関数電卓で解いてみよう.

解答例題 4.1

$y = f (x)$ の 1 階, 2 階の導関数は以下のとおりである.

f^{'} (x) = 3 x^{2} - 3, f^{''} = 6 x

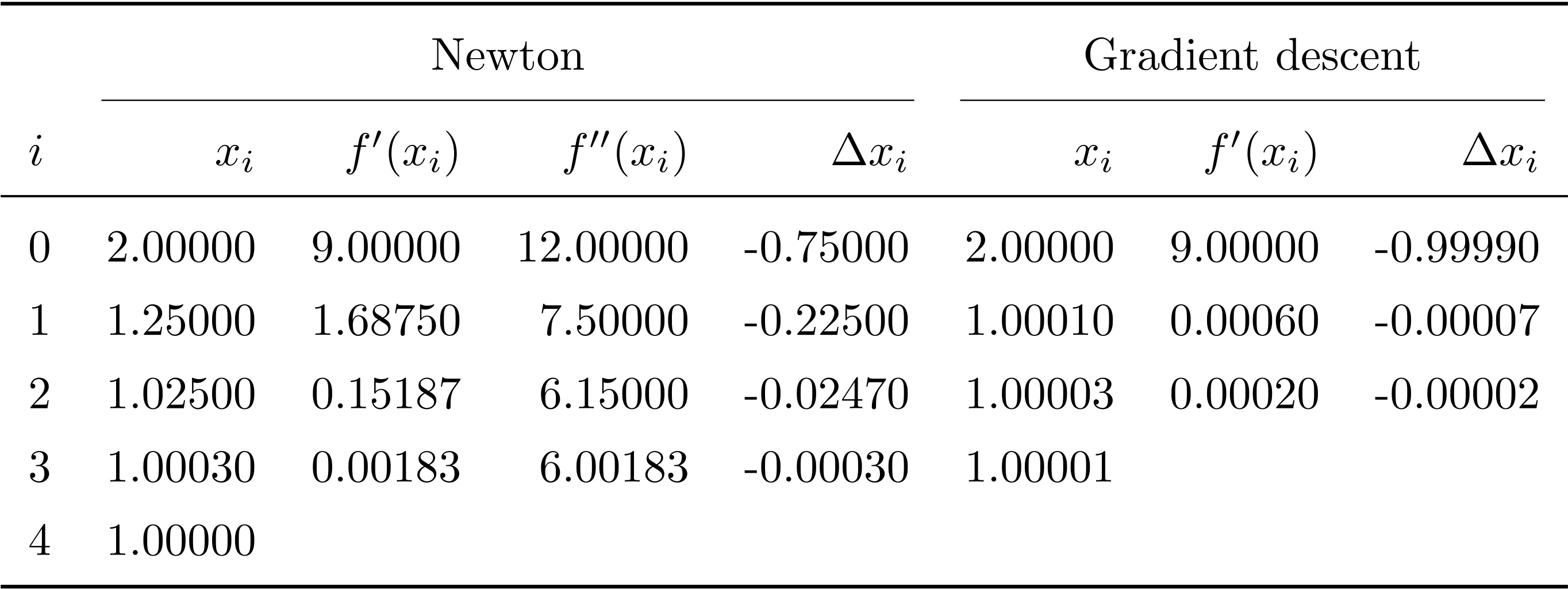
$x_{0} = 2$ として, それぞれのアルゴリズムに従って, $f^{'} (x_{i})$ , $f^{''} (x_{i})$ を計算し, それらをもとに Newton 法では $Δ x_{i} = f^{'} (x_{i}) / f^{'' (x_{i})}$ , 勾配降下法では $Δ x_{i} = - η f^{'} (x_{i})$ を算出. そこから $x_{i + 1} = x_{i} + Δ x_{i}$ を算出した. 結果を表 3 勾配降下法における初期値と学習率の影響の例にまとめた.

表 1 例題 4.1 の計算

備考 4.2

以上の操作で, Newton 法と勾配降下法で $x_{i}$ が近似解に近づいていく様子がよく分かる. この問題の場合, 勾配降下法のほうが, Newton 法より速く収束した. 勾配法でも, 学習率をうまく選べば, 収束を早めることができる. ただし, ここでは収束条件を $ε_{0} = 1.0 \times 10^{- 4}$ とかなり緩いものにした. 例えばこれを $1.0 \times 10^{- 6}$ に変えると Newton 法のほうが速くなる.

一般に, Newton 法は近似解への収束が速いことが知られている. これに対し, 勾配降下法は収束速度が遅いが, 1 階微分を計算するだけでよいのが大きなメリットとなる. 特に機械学習など変数の数 $n$ が大きい場合には, 2 解微分である Hessian の計算に $n^{2}$ の計算が必要となることを考えると, 勾配降下法が選ばれる理由が納得できる.

初期値依存性

非線形の最適化問題は, 初期値の選び方が重要である. 領域内の「最小点」を選ぶ問題の場合, 初期値の選び方によっては, 最小点とは別の極小点が解として得られてしまう場合もあれば, 全く解が得られない（発散する）場合もある.

大まかな傾向とすれば, 目的とする極小値（例えば最小値）の近くに初期値を持ってくると, その点に収束する場合が多い. しかし, 勾配降下法などでは適切な学習率を設定しないと, 初期値が解の近くにあっても $x_{i}$ が解に収束しない場合がある（後述）.

また, そもそもの問題として, 解が未知なのだから, 初期値をその近くに設定するというのは無理がある. このため, 往々にして様々な初期値を試すことになる. このあたりに非線形最適化問題の難しさがある.

まずは Newton 法で初期値依存性をみよう.

例題 4.2

の次の関数の停留点を求めるのに Newton 法を用いる.

\begin{array}{r} y = f (x) = x^{3} - 3 x \end{array}

初期値を $x_{0} = - 0.1, 0.1$ としたときに, それぞれ, どのような停留点に収束するか.

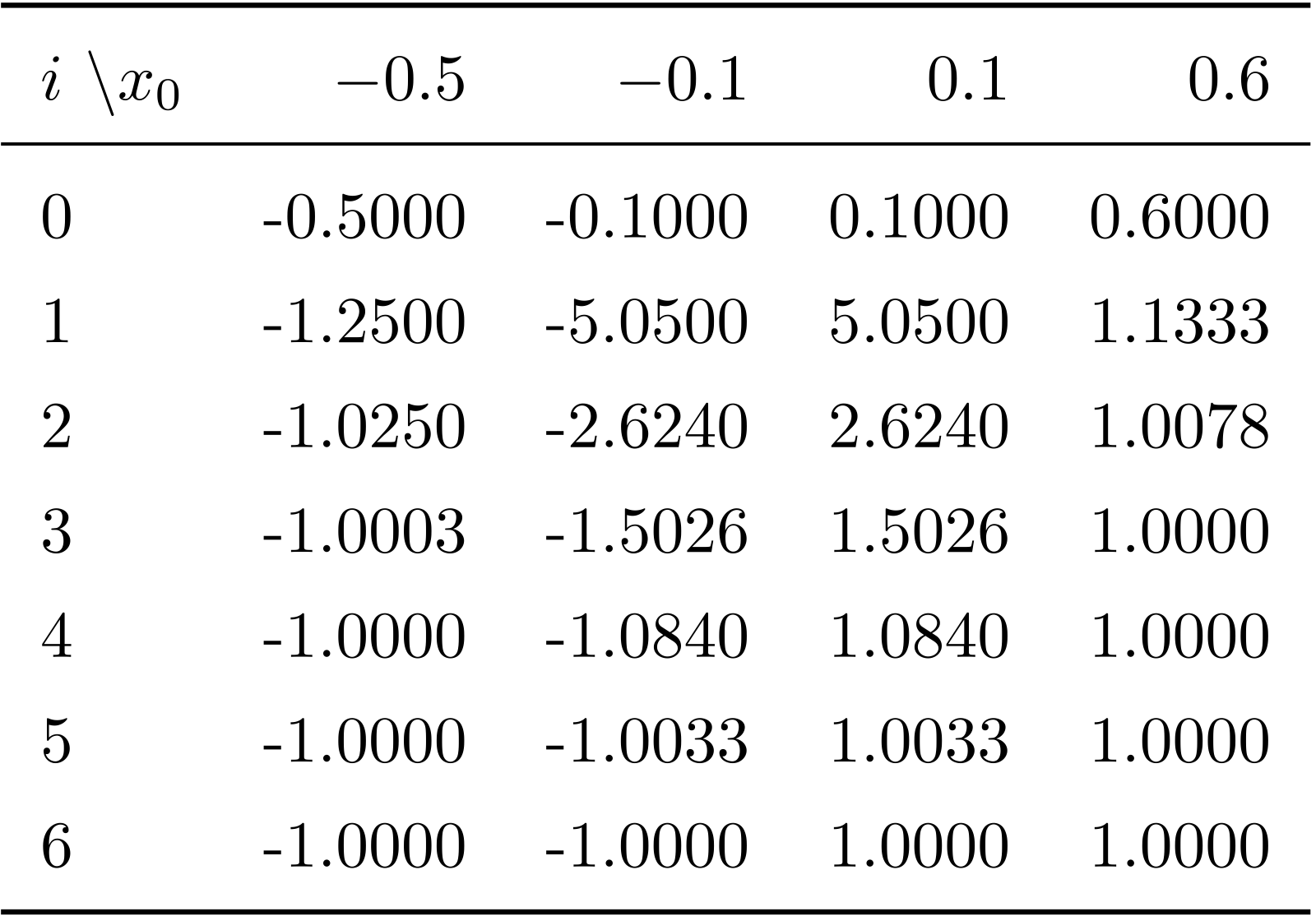
解答例題 4.2 実際に Newton 法で計算してみると（表 2 Newton 法の初期値依存性） $x_{0} = - 0.1$ のときには, $x = - 1$ に, $x_{0} = 0.1$ のときには $1$ に収束することが分かる.

備考 4.3

Newton 法は, 停留点 $d f / d x = 0$ を求める方法なので, 極大点にも収束する. 表 2 Newton 法の初期値依存性に, $x_{0} = - 0.5, - 0.1, 0.1, 0.6$ のときに, $x_{6}$ までを計算した結果を示す. 図を描いてみれば分かるが, この関数の変曲点 $x = 0$ より初期値 $x_{0}$ が小さければ極大点 $x = - 1$ に収束し, 大きければ極小点 $x = 1$ に収束する. $x_{0} = - 0.5$ のほうが, $x_{0} = - 0.1$ よりも $x = - 1$ に近いので, 前者の場合のほうが収束が速い. また, この関数は原点まわりで点対称なので, 初期値 $x_{0}$ の絶対値が同じであれば, 符号以外の結果は同じになる. これを踏まえて, $x_{0} = - 0.5$ と $x_{0} = 0.6$ を比較すると, $| - 1 - (- 0.5) | > | 1 - 0.6 |$ なので, 後者のほうが速く収束する.

表 2 Newton 法の初期値依存性

例 4.4

例題 4.1 の関数

\begin{array}{r} y = f (x) = x^{3} - 3 x \end{array}

に勾配降下法を適用する. 様々な初期値と学習率の組で計算を行った場合の $i = 8$ までの $x_{i}$ を表 1 例題 4.1 の計算にまとめた.

表 3 勾配降下法における初期値と学習率の影響の例

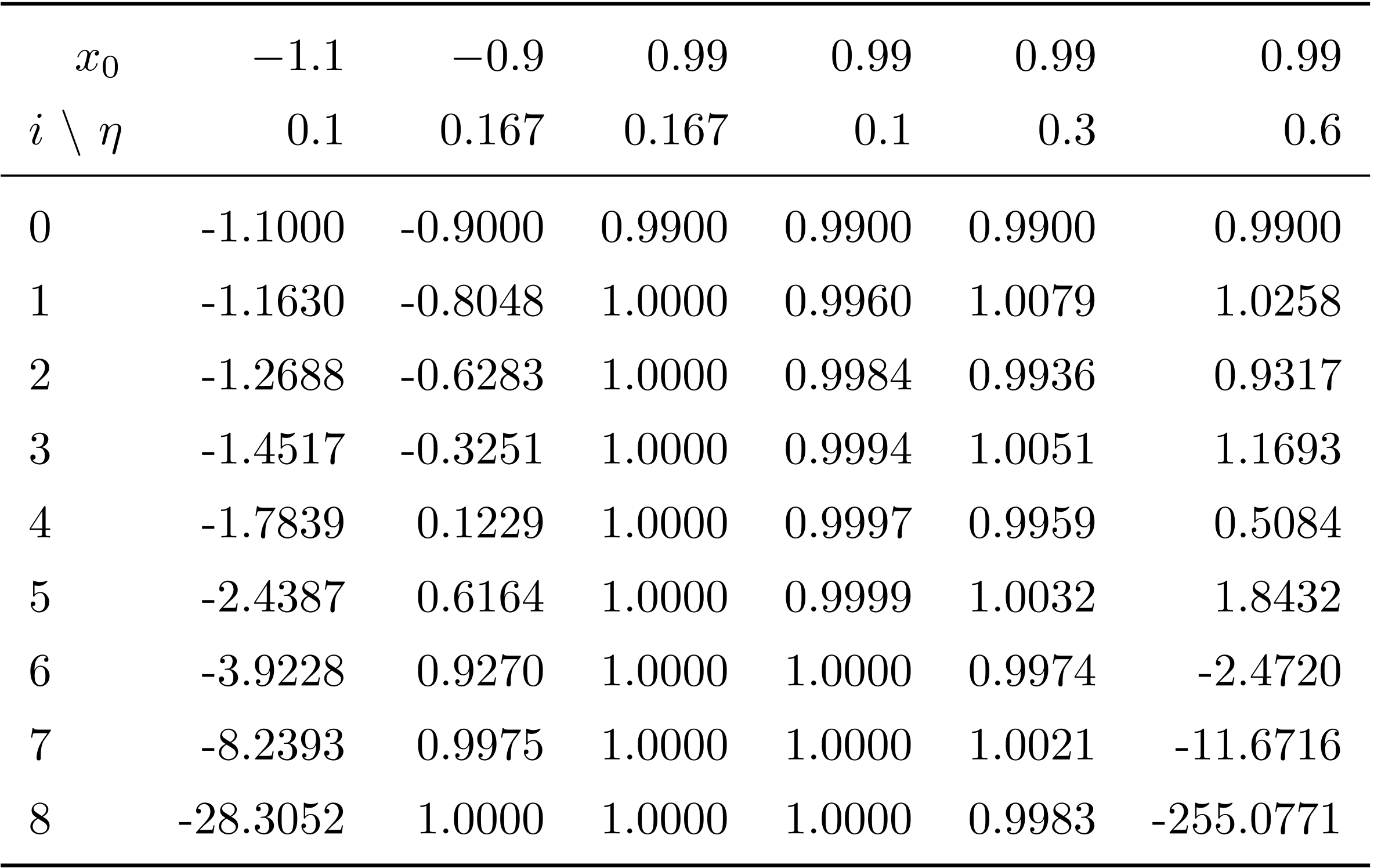
勾配降下法では, 初期値 $x_{0}$ と学習率 $η$ の両方によって収束が違ってくる. 左から見ていこう. 初期値と学習率が $x_{0} = - 1.1$ , $η = 0.1$ の場合, 初期値が極大点 $- 1$ より小さいので, 勾配を下ると, $x$ はどんどん負の方向に移動する. よって発散してしまう. $x_{0} = - 0.9$ , $η = 0.167$ のときは, 初期値は極大値より右なので収束する. 学習率はこれが最適だが, 収束は遅い. $x_{0} = 0.99$ の場合, 学習率を最適, 0.1, 0.3, 0.6 と変化させてその影響をみた. 最適学習率 $η = 0.167$ の場合, $x_{1}$ ですでに誤差が $5 \times 10^{5}$ 以下になっている. $η = 0.1$ の時には, 同じようなレベルになるのに 6 回かかっている. $η = 0.3$ の場合, $x_{i}$ は, $x_{i} > 1$ , $x_{i} < 1$ を繰り返してながら $x = 1$ に近づいている. この場合はいずれ収束するが, このように $x_{i}$ が振動する場合は学習率が大きすぎると考えてよい. $η = 0.6$ の場合, $x_{i}$ は, $x_{i} > 1$ , $x_{i} < 1$ を繰り返してながら発散し, $x_{i} < - 1$ となったところから勾配を降ってどんどん負の方向に移動することになる.

多変数関数の場合

2 変数関数のゼロ点と停留点

第 1 章で見たように, 2 変数以上の多変数関数の極大・極小問題はすべて同じように扱える. よって, ここでは 2 変数関数のみ考える. 次の関数を考えよう.

\begin{array}{r} y = f (x, y) = x^{2} + y^{2} - 1 \end{array}

この関数のゼロ点は $x^{2} + y^{2} - 1 = 0$ の解だから, 原点を中心として半径を 1 とする円となる. つまり, この関数のゼロ点は 1 点には定まらない. 一方, 停留点は

\begin{array}{r} \frac{\partial f}{\partial x} = 2 x = 0, \frac{\partial f}{\partial y} = 2 y = 0 \end{array}

の解なので, $(x, y) = (0, 0)$ と 1 点に定まる. 停留点が極大値を与えるか極小値を与えるか等については, 第 1 章で解説した方法で調べればよい. 以上を考えて, この節では Newton 法でもゼロ点はとりあげず, 停留点と極小点のみを議論する.

Newton 法による停留点の求め方（2 変数）

1 変数の場合と, アルゴリズムは同じになる. ただし, $f$ が多変数関数なので, $x_{i}$ がベクトル $x_{i} = {[x_{i}, y_{i}]}^{T}$ に変わるほか, $x_{i}$ の更新の部分（1 変数の場合は $Δ x_{i} = - f^{'} (x_{i}) / f^{''} (x_{i})$ ）が次のように変わる.

(31)

\begin{array}{r} x_{i + 1} = x_{i} + Δ x_{i}, Δ x_{i} = - H_{f} (x_{i})^{- 1} \nabla f (x_{i}) \end{array}

ここで, $H_{f}$ は第 1 章でもとりあげた Hesse 行列である. 関数 $f$ の Hesse 行列であることを強調したいために, 添字として $f$ を付けてある. $H (x_{i})^{- 1}$ は $x_{i}$ における Hesse 行列の逆行列である. $\nabla f (x_{i})$ は, 次に示す勾配(gradient）である. 勾配は $\nabla f$ とか $grad f$ で表される.

\begin{array}{r} \begin{matrix} \nabla f (x_{i}) = grad f (x_{i}) = [\begin{array}{c} \frac{\partial f}{\partial x} (x_{i}) \\ \frac{\partial f}{\partial y} (x_{i}) \end{array}] \end{matrix} \end{array}

式 (31) の $Δ x_{i}$ は, $2 \times 2$ 行列 $H (x_{i})^{- 1}$ と 2 項列ベクトル $\nabla f (x_{i})$ の積だから, 2 項列ベクトルとなる.

これだけでは分かりにくいだろうから, 簡単な計算例をみていこう.

例 4.5

\begin{array}{r} y = f (x, y) = x^{2} + y^{2} + x^{2} y^{2} \end{array}

の停留点は $x = {[0, 0]}^{T}$ だが, 初期値を $x_{0} = {[2, 1]}^{T}$ として Newton 法で求める最初のステップを調べる.

\begin{array}{r} \begin{matrix} \nabla f (x) = [\begin{array}{c} \begin{array}{r} 2 x + 2 x y^{2} \\ 2 y + 2 x^{2} y \end{array} \end{array}], H_{f} (x) = [\begin{array}{c} \begin{array}{rr} 2 + 2 y^{2} & 4 x y \\ 4 x y & 2 + 2 x^{2} \end{array} \end{array}] \end{matrix} \end{array}

さて, $x_{0} = {[2, 1]}^{T}$ のときに

\begin{array}{r} \begin{matrix} \nabla f (x_{0}) = [\begin{array}{c} \begin{array}{r} 8 \\ 10 \end{array} \end{array}], H_{f} (x_{0}) = [\begin{array}{c} \begin{array}{rr} 4 & 8 \\ 8 & 10 \end{array} \end{array}], H_{f} (x_{0})^{- 1} = [\begin{array}{c} \begin{array}{rr} - 5 / 12 & 1 / 3 \\ 1 / 3 & - 1 / 6 \end{array} \end{array}] \end{matrix} \end{array}

\begin{array}{r} \begin{matrix} Δ x_{0} = - H_{f} (x_{0})^{- 1} \nabla f (x_{0}) = - [\begin{array}{c} \begin{array}{rr} - 5 / 12 & 1 / 3 \\ 1 / 3 & - 1 / 6 \end{array} \end{array}] [\begin{array}{c} \begin{array}{r} 8 \\ 10 \end{array} \end{array}] = [\begin{array}{c} \begin{array}{r} 0 \\ - 1 \end{array} \end{array}] \end{matrix} \end{array}

\begin{array}{r} \begin{matrix} x_{1} = x_{0} + Δ x_{0} = [\begin{array}{c} \begin{array}{r} 2 \\ 1 \end{array} \end{array}] + [\begin{array}{c} \begin{array}{r} 0 \\ - 1 \end{array} \end{array}] = [\begin{array}{c} \begin{array}{r} 2 \\ 0 \end{array} \end{array}] \end{matrix} \end{array}

あとは, $x_{i}$ の更新を繰り返せばよい.

勾配降下法による極小点の求め方（2 変数）

勾配降下法の場合も, $f^{'} (x_{i})$ が $\nabla f (x_{i})$ となるだけで, アルゴリズムは同じである. 学習率はスカラーのままでよい.

\begin{array}{r} x_{i + 1} = x_{i} + Δ x_{i}, Δ x_{i} = - η \nabla f (x_{i}) \end{array}

例 4.6

例 4.5 と同じ関数

\begin{array}{r} y = f (x, y) = x^{2} + y^{2} + x^{2} y^{2} \end{array}

の関数の極小点を勾配降下法で求る最初のステップを示そう.

ただし学習率は $η = 0.05$ とする.

例 4.5 でみたように, 勾配は, $\nabla f = {[2 x + 2 x y^{2}, 2 y + 2 x^{2} y]}^{T}$ だから, 初期値 $x_{0} = {[2, 1]}^{T}$ に対して

\begin{array}{r} \begin{matrix} \nabla f (x_{0}) = [\begin{array}{c} \begin{array}{r} 8 \\ 10 \end{array} \end{array}], Δ x = - η \nabla f (x_{0}) = [\begin{array}{c} \begin{array}{r} - 0.4 \\ - 0.5 \end{array} \end{array}] \end{matrix} \end{array}

\begin{array}{r} \begin{matrix} x_{i + 1} = x_{i} + Δ x_{i} = [\begin{array}{c} \begin{array}{r} 2 \\ 1 \end{array} \end{array}] + [\begin{array}{c} \begin{array}{r} - 0.4 \\ - 0.5 \end{array} \end{array}] = [\begin{array}{c} \begin{array}{r} 1.6 \\ 0.5 \end{array} \end{array}] \end{matrix} \end{array}

あとは, $x_{i}$ の更新を繰り返すことになる.

収束判定（多変数）

多変数の場合の収束判定は, 1 変数の場合と違って, ベクトル $\nabla (x_{i})$ の大きさを調べることになる. これにはいくつかの方法があるが, $ξ = {[ξ_{1}, \dots, ξ_{n}]}^{T}$ のユークリッドノルム

\begin{array}{r} {‖ ξ ‖}_{2} = \sqrt{ξ_{1}^{2} + \dots + ξ_{n}^{2}} \end{array}

は, 変数の数が多くなると, 計算コストが高い. そのためだろうが, 多くの場合, 次の最大値ノルムが用いられる.

\begin{array}{r} {‖ ξ ‖}_{\infty} = max | ξ_{i} | \end{array}

アルゴリズム

整理の意味もこめて, 多変数の Newton 法と勾配降下法のアルゴリズムを載せる.

../_images/fig_algorithm_newton_multi.png — 図 27 多変数関数で Newton 法により停留点を求めるアルゴリズム

../_images/fig_algorithm_GD_multi.png — 図 28 多変数関数で勾配降下法により極小点を求めるアルゴリズム

Python による計算例

はじめに

Newton 法にせよ勾配降下法にせよ, 1 変数の場合はともかく, 多変数の場合はコンピューターを使って計算すべきものである. このとき, 勾配などを計算する必要があるが, 特に Newton 法の場合, Hesse 行列, 及びその逆行列を計算する必要があり, これを一々入力するのは大変である. このようなとき, 自動微分関連のパッケージを用いればよい.

ここでは, Google 製の JAX（https://github.com/google/jax）を使う. JAX は自動微分と高速化線形代数をひとつにしたパッケージであり, 色々なことができるのだが, ここでは, numpy の機能を代替する $jnp.numpy$ と, 自動微分の機能のみを使う. 自動微分を使うだけで, 最適化計算にかかる労力の大半を削減することができる.

Newton 法の計算例（2 変数）

ここでは, 次の関数の停留点を初期値 $x_{0} = [0.2, 2.2]^{T}$ として Newton 法で解く.

\begin{array}{r} z = f (x, y) = - \cos (2 x) \sin (y) \end{array}

{language=Python}
import jax  # jax パッケージを使う
import jax.numpy as jnp  # numpy の代わりに jax.numpy を使う.
from jax import config  # この行と次の行は jax での 64-bit 浮動小数点計算のため
config.update("jax_enable_x64", True)


def func(x):
    return - jnp.cos(2 * x[0]) * jnp.sin(x[1])


# jax では, Hesse 行列を計算する関数がないので作る.
def jax_hess(f):
    return jax.jacfwd(jax.jacrev(f))


def main():
    eps_0 = 1.e-15  # 収束条件の設定
    x = jnp.array([.2, 2.2])  # 初期値の設定
    # 最大値ノルムの計算
    nrm_grad = jnp.linalg.norm(jax.grad(func)(x), ord=jnp.inf)
    while nrm_grad > eps_0:
        grad = jax.grad(func)(x)
        hess = jax_hess(func)(x)
        hess_inv = jnp.linalg.inv(hess)  # Hesse 行列の逆行列
        dltx = jnp.matmul(hess_inv, grad) # H_f^-1 と grad f の積
        x = x - dltx
        print(x)
        nrm_grad = jnp.linalg.norm(grad, ord=jnp.inf)
    # 極大・極小判定のため Hessian matrix の 固有値を出力
    print(jnp.linalg.eigvals(hess))


if __name__ == '__main__':
    main()

出力は以下の通り.

{language=Python}
    [-0.15723497  1.25222653]
    [0.02518525 1.62116685]
    [-8.55469635e-05  1.57062523e+00]
    [3.33897023e-12 1.57079633e+00]
    [0.         1.57079633]
    [0.         1.57079633]
    [4.+0.j 1.+0.j]

出力から, 停留点として $[0, 1.57]^{T}$ が得られ, Hesse 行列の固有値が 4, 1, で共に正だから, これが極小点であることが分かる.

演習問題

問題 4.1

次の関数の極小点を $x \in (0, 2)$ の範囲で求めるために, 例題1 と同様のやり方で $x_{4}$ までの各値を求めて表にせよ. ただし, 初期値は $x_{0} = 2$ とし, 勾配降下法の学習率は $η = 0.033$ とせよ.

\begin{array}{r} y = f (x) = x^{4} - 6 x^{2} \end{array}

問題 4.2

次の関数の停留点を Newton 法で求める. 1) 関数 $y = f (x)$ のグラフを $x \in (- 1.5, 1.5)$ の範囲で描け. 2) 初期値 $x_{0} = - 3, - 1, 0.3, 2$ から初めたとき, 解はどの停留点に収束するか.

(32)

\begin{array}{r} y = f (x) = x^{4} - 2 x^{2} \end{array}

ちなみに, 停留点は,

y = f^{'} (x) = 4 x^{3} - 4 x = 0

の解なので, $x = - 1, 0, 1$ の 3 つである. また, 変曲点は

y = f^{''} (x) = 12 x^{3} - 4 = 0

の解であるから, $x = \pm 1 / \sqrt{3}$ である.

問題 4.3

（この問題は Python を使うほうがよい.）上記の式 (32) の関数の極小点を勾配降下法で求めることにする. グラフの形から, 初期値を正の数にとると, 極小値 $x = 1$ に, 初期値を負の値にとると, 極小値 $x = - 1$ に収束するはずである. 1) 初期値を負にとり, その値で $x = - 1$ に収束するように学習率 $η$ を定めよ. 2) 初期値を正にとり, その値で $x = 1$ に収束するように学習率 $η$ を求めよ. 3) 上記 1), 2) のいずれかにおいて, 学習率 $η$ を変えたときに, 収束速度がどのように変化するか計算例を示せ.

◀ Previous

TOC

微分積分・線形代数の次に学ぶ数学