微分積分・線形代数の次に学ぶ数学
Takuya Kawanishi
◀ Previous TOC Next ▶

連立線形微分方程式

この章で学ぶこと

  • 連立線形微分方程式（線形微分方程式系）とその解

  • 行列の指数関数

  • 線形微分方程式系の解の挙動

    • 固有値が実数で対角化可能な場合

    • 固有値が実数で縮退している場合

    • 固有値が共役複素数の場合

  • 力学系の入門

連立線形微分方程式

この章で考える連立線形微分方程式

この章では, 次のような連立微分方程式を考える. \(\boldsymbol x = \left[x_1, \dotsc, x_n\right]^\mathrm T\) を \(n\) 項列ベクトルとする [1]. \(\boldsymbol x\) に関する1階の微分方程式と初期条件を次のように表す.

(18)\[\begin{split} \frac{d \boldsymbol x}{d t} = A \boldsymbol x, \quad \boldsymbol x(0) = \boldsymbol x_0, \quad t \in [0, \infty), \ \boldsymbol x \in (-\infty, \infty)^n \end{split}\]

ここで

\[\begin{split}\begin{split} \frac{d \boldsymbol x}{d t} = \begin{bmatrix} \begin{array}{c} \dfrac{d x_1}{dt} \\ \vdots \\ \dfrac{d x_n}{dt} \end{array} \end{bmatrix}, \quad A = \begin{bmatrix} \begin{array}{ccc} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{n1} & \cdots & a_{nn} \end{array} \end{bmatrix}, \quad \boldsymbol x(0)= \boldsymbol x_0= \begin{bmatrix} \begin{array}{c} x_{1,0}\\ \vdots \\x_{n, 0} \end{array} \end{bmatrix} \end{split}\end{split}\]

ただし \(a_{ij}\) は実定数とする. この微分方程式系は, 定係数同次1階連立微分方程式とよばれる. \(\boldsymbol x_0\) が与えられているので, 初期値問題である.

英語では, 連立線形微分方程式を system of linear differential equations という. しばしば, 線形微分方程式系と訳される.

1変数の場合の解と連立微分方程式の解の比較

まずは, 1 変数の場合, すなわち \(dx/dt = ax\) , \(x(0)=x_0\) の場合の解と \(n\) 変数の場合（式(18) ）の解を定理として提示し, その後に解説をすることにしよう. ちなみに, 1変数の場合は変数分離法でも解けるし, 1階線形微分方程式の解の公式を用いても解ける. 解法が気になる人は微分方程式の教科書を参照して欲しい. ただ, 理工系を志す人ならば, 次の式(19) を見ただけで, 解(20) がすぐ出てくるようになってほしい.

定理 3.1

1変数1階線形微分方程式の初期値問題 （\(x, x_0, t \in [0, \infty)\) , \(a\) は定数）

(19)\[\begin{split} \frac{d x}{d t} = a x, \quad x(0) = x_0 \end{split}\]

の解は

(20)\[\begin{split} x = e^{at} x_0 \quad \qquad \Box \end{split}\]

定理 3.2

線形微分方程式系の初期値問題（\(\boldsymbol x, \boldsymbol x_0 \in \mathbb R^n\) , \(t \in [0, \infty)\) , \(A \in \mathbb R^{n \times n}\) は実定数行列）

\[\begin{split} \frac{d \boldsymbol x}{d t} = A \boldsymbol x, \quad \boldsymbol x(0) = \boldsymbol x_0 \end{split}\]

の解は

(21)\[\begin{split} \boldsymbol{x}= e^{A t}\boldsymbol{x}_0 \qquad \Box \end{split}\]

解 (20) と解 (21) とはほとんど同じ形をしている. 違いは, 指数関数が式 (20) では, \(e^{at}\) なのに対して, 式 (21) では \(e^{At}\) となっていることである. このように, 多変数になっても, 解の形が1変数と似たような形になることは, 線形微分方程式系の挙動にある見通しを与えることになる. しかし, そもそも \(e^{At}\) は何を表しているのだろうか.

行列の指数関数

行列の指数関数の定義

指数関数については, いくつか異なった定義のしかたがあるが, 級数による定義は複素数 \(a\) に対しても成り立つ. 行列の指数関数は, この定義の \(a\) を行列に置き換えたもので定義される.

定義 3.3

\[\begin{split} e^a (= \exp a)=\sum_{k=0}^\infty \frac{a^k}{k!} \ = 1 + a + \frac{1}{2} a^2 + \frac{1}{6} a^3+\dotsb \end{split}\]

定義 3.4 行列の指数関数, matrix exponential

\(A\) を \(n \times n\) 行列とするとき（単位行列を \(E\) として）

\[\begin{split} e^A (= \exp A) = \sum_{k=0}^\infty \frac{A^k}{k!} \ = E + A + \frac{1}{2}A^2 + \frac{1}{6} A^3 + \dotsb \end{split}\]

例 3.5 対角行列の指数関数

対角行列

\[\begin{split}\begin{split} J = \begin{bmatrix} \begin{array}{ccc} d_1 & & 0 \\ & \ddots & \\ 0 & & d_n \end{array} \end{bmatrix} \end{split}\end{split}\]

に対し \(e^{tJ}\) は

(22)\[\begin{split}\begin{split} e^{tJ} = \begin{bmatrix} \begin{array}{ccc} e^{t d_1} & & 0 \\ & \ddots & \\ 0 & & e^{td_n} \end{array} \end{bmatrix} \end{split}\end{split}\]

例題 3.1

次に与える \(A\) , \(\boldsymbol x_0\) の定める初期値問題 \(\frac{d\boldsymbol x}{d t} = A \boldsymbol x\) , \(\boldsymbol x(0) = \boldsymbol x_0\) の解を求めよ.

\[\begin{split}\begin{split} A = \begin{bmatrix} \begin{array}{rr} -1 & 0 \\ 0 & 2 \end{array} \end{bmatrix}, \quad \boldsymbol x_0 = \begin{bmatrix} \begin{array}{c} 1 \\ 1 \end{array} \end{bmatrix} \end{split}\end{split}\]

解答 例題 3.1 初期値問題の解は式(21) で与えられる. \(A\) は対角行列だから, 式(22) を使って

\[\begin{split}\begin{split} \boldsymbol x(t) = e^{tA} \boldsymbol x_0 = \begin{bmatrix} \begin{array}{cc} e^{-t} & 0 \\ 0 & e^{2t} \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{c} 1 \\ 1 \end{array} \end{bmatrix} = \begin{bmatrix} \begin{array}{c} e^{-t} \\ e^{2t} \end{array} \end{bmatrix} \end{split}\end{split}\]

実固有値の正方行列は標準形にできる

さて, 前項で行列の指数関数を定義し対角行列の指数関数を例として示した. 対角行列の場合は行列の指数関数の計算も, それを用いた解の挙動の解析も簡単である. 一般の行列も対角化できるならば基底変換（座標変換）により指数行列の部分は簡単になる. まずは線形代数から次の定理を引こう.

定理 3.6

\(n \times n\) 実数行列 \(A\) の固有値がすべて実数の場合, この行列はある行列 \(P\) によって, 必ず Jordan 標準形 \(J_\mathrm c=P^{-1} A P\) に変形できる.

備考 3.7

Jordan 標準形は, Jordan 細胞を対角に並べたものである. 例として, 1, 2, 3 次の Jordan 細胞 \(J_1\) , \(J_2\) , \(J_3\) を次に示そう.

\[\begin{split}\begin{split} J_1 = \begin{bmatrix} \begin{array}{c} \lambda \end{array} \end{bmatrix}, \quad J_2 = \begin{bmatrix} \begin{array}{cc} \lambda & 1 \\ 0 & \lambda \end{array} \end{bmatrix}, \quad J_3 = \begin{bmatrix} \begin{array}{ccc} \lambda & 1 & 0 \\ 0 & \lambda & 1 \\ 0 & 0 & \lambda \end{array} \end{bmatrix} \end{split}\end{split}\]

このように, \(r\) 次の Jordan 細胞は, 対角に \(r\) 個の固有値 \(\lambda\) が並び, その 1 つ上の行に1 が入る行列となる. \(n \times n\) 行列のJordan 標準形 \(J_\mathrm c\) は

\[\begin{split}\begin{split} J_\mathrm c = \begin{bmatrix} \begin{array}{cccc} J_{k_1} & & & \\ & J_{k_2} & & \\ & & \ddots & \\ &&& J_{k_l} \end{array} \end{bmatrix} \end{split}\end{split}\]

ここで

\[\begin{split} k_1 + k_2 + \dotsb + k_l = n \end{split}\]

また, 各 Jordan 細胞 \(J_{k_i}\) の対角成分には, それぞれの固有値が入る.

備考 3.8

対角行列は, 1 次の Jordan 細胞を対角に並べたものだから, Jordan 標準形である. つまり, Jordan 標準形は対角行列を含む.

対角化可能行列の指数関数の計算法

ここでは, 固有値がすべて実数の行列について, 行列が対角化できる場合と, 対角化できない, つまり Jordan 細胞を含む形にしか変形できない場合に分けて, 行列の指数関数の求め方を示そう. まずは, 行列が対角化できる場合について述べる.

命題 3.9 正方行列の対角化

行列 \(A \in \mathbb R^{n\times n}\) が対角化できるとき, 対角化行列 \(J\) は, 列固有ベクトルを並べた行列 \(P\) を用いて次のように表される.

\[\begin{split} J = P^{-1} A P \quad \qquad \Box \end{split}\]

例題 3.2 対角行列のべき

\(J = P^{-1} A P\) と対角化されるとき, 対角化行列 \(J\) のべき \(J^n\) について以下が成立することを示せ.

(23)\[\begin{split} J^n = P^{-1} A^n P \end{split}\]

解答 例題 3.2 対角行列のべき

\[\begin{split}\begin{split} J^n = (P^{-1} A P)^n %\\ & = \underbrace{ (P^{-1} A \underbrace{P)(P^{-1}}_{E} A P) \dotsm (P^{-1} A P) }_n = P^{-1} A^n P \end{split}\end{split}\]

式(23) の両辺に左から \(P\) を, 右から \(P^{-1}\) をかけることによって, \(A^n\) に関する次の結果が得られる.

定理 3.10

\(J\) に対角化されるとき,

(24)\[\begin{split} \boxed{ A^n = P J^n P^{-1} } \end{split} \qquad \Box\]

例題 3.3

\[\begin{split}A = \begin{bmatrix} \begin{array}{rr} \frac{5}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{5}{2} \end{array} \end{bmatrix}\end{split}\]

解答 例題 3.3 まず \(A\) を対角化する. 固有方程式 \(\det (A - \lambda E) = 0\) より

\[\begin{split} \lambda^2 - 5 \lambda - 6 = 0 \end{split}\]

固有値は \(\lambda_1 = 3\) , \(\lambda_2 = 2\) . まず, \(\lambda_1 = 3\) に対応する固有ベクトルは, 行列の第1行と \(\left[x, y \right]^\mathrm T\) の積が \(\lambda_1 x\) に等しいことから

\[\begin{split} \frac{5}{2} x + \frac{1}{2} y = 3 x \end{split}\]

より, 例えば \([1, 1]^{\mathrm T}\) , \(\lambda_2 = 2\) に対応する固有ベクトルは

\[\begin{split} \frac{5}{2} x + \frac{1}{2} y = 2 x \end{split}\]

より, 例えば \([1, -1]^{\mathrm T}\) . これより, \(P\) として次の行列をとることができる.

\[\begin{split}\begin{split} P = \begin{bmatrix} \begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array} \end{bmatrix} \end{split}\end{split}\]

この逆行列は

\[\begin{split}\begin{split} P^{-1} = \begin{bmatrix} \begin{array}{rr} \frac{1}{2} & \frac{1}{2} \\ - \frac{1}{2} & \frac{1}{2} \end{array} \end{bmatrix} \end{split}\end{split}\]

よって, 対角化行列 [2] は

\[\begin{split}\begin{split} J = P^{-1} A P = \begin{bmatrix} \begin{array}{rr} 3 & 0 \\ 0 & 2 \end{array} \end{bmatrix} \end{split}\end{split}\]

行列のべき \(A^5\) は式 (24) に上記 \(J\) と \(n=5\) を代入して

\[\begin{split}\begin{split} A^5 = P J^5 P^{-1} & = \begin{bmatrix} \begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} 3^5 & 0 \\ 0 & 2^5 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & - \frac{1}{2} \end{array} \end{bmatrix} %\\ & %= \begin{bmatrix} 243 & 32 \\ 243 & -32 \end{bmatrix} \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} \end{bmatrix} %\\ & = \begin{bmatrix} \begin{array}{rr} \frac{275}{2} & \frac{211}{2} \\ \frac{211}{2} & \frac{275}{2} \end{array} \end{bmatrix} \end{split}\end{split}\]

また, 行列の指数関数の定義より, 次の重要な結果が得られる.

定理 3.11

（\(A \in \mathbb R^{n \times n}\) ）が \(J= P^{-1} A P\) と対角化可能なとき,

\[\begin{split} \boxed{ e^{tA} = P e^{tJ} P^{-1}} \end{split} \qquad \Box\]

備考 3.12

\(t\) がスカラー（scalar) のとき, \(e^{tA} = e^{At}\) である. どちらの表記も可.

Proof.

\[\begin{split}\begin{aligned} e^{tJ} &= e^{(P^{-1} A P) t} \\ & = E + (P^{-1} A P) t + \frac{(P^{-1}A P)^2 t^2}{2!} + \dotsb + \frac{(P^{-1} A P)^k t^k}{k!} + \dotsb \\ & = P^{-1} E P + P^{-1} (At) P + \frac{P^{-1} A^2 t^2 P}{2!} + \dotsb + \frac{P^{-1} A^kt^k P}{k!} + \dotsb \\ & = P^{-1} \left( E + At + \frac{A^2 t^2}{2!} + \dotsb + \frac{A^k t^k}{k!} + \dotsb\right) P %\\ & = P^{-1} e^{tA} P\end{aligned}\end{split}\]

この両辺に左から \(P\) , 右から \(P^{-1}\) をかけて

\[\begin{split} P e^{tJ} P^{-1} = e^{tA} \qquad \Box \end{split}\]

 ◻

上記の計算では

\[\begin{split} (P^{-1}A P)^2 = P^{-1} A \underbrace{P P^{-1}}_{=E} A P = P^{-1} A^2 P \end{split}\]

等を使っている. 第1章と同じである.

対角化できない行列の指数関数の計算法

固有値がすべて実数の正方行列は, 対角化できない場合には, Jordan 細胞を含む Jordan 標準形に変形できる（ 定理 3.6 ）. この場合も, 対角化できる場合と全く同じ議論で, \(e^{tA}\) が計算できる.

定理 3.13

\((A \in \mathbb R^{n\times n}\) が \(J_\mathrm c = P^{-1} A P\) と標準化されるとき

\[\begin{split} e^{tA} = P e^{tJ_\mathrm c} P^{-1} \quad J_\mathrm c \text{ は Jordan 標準形} \end{split}\qquad \Box\]

例えば, 上記の2次の Jordan 細胞の場合, \(e^{tJ_2}\) は次のようになる.

\[\begin{split}\begin{split} e^{tJ_2} = \begin{bmatrix} \begin{array}{rr} e^{ta} & t e^{ta} \\ 0 & e^{ta} \end{array} \end{bmatrix} \end{split}\end{split}\]

固有値が実数の場合の解の挙動

解の時間変化は \(e^{tJ}\) で決まる

行列 \(A\) が \(J = P^{-1} A P\) と対角化できる場合, 定理 3.2 と 定理 3.11 から, 連立微分方程式の初期値問題の解については以下が成立する.

(25)\[\begin{split} \boldsymbol x(t) = e^{tA} \boldsymbol x_0 = P e^{tJ} P^{-1} \boldsymbol x_0 \end{split}\]
(26)\[\begin{split}\begin{split} e^{tJ} = \begin{bmatrix} \begin{array}{cccc} e^{\lambda_1 t} & 0 &\cdots & 0\\ 0 & e^{\lambda_2 t} &\cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & e^{\lambda_n t} \end{array} \end{bmatrix} \end{split}\end{split}\]

さて, この解の形から分かるように, 時間 \(t\) は, \(e^{tJ}\) の部分のみ影響する.

\[\begin{split} \boldsymbol x(t) = P \underbrace{e^{tJ}}_{\text{時間依存はここだけ}}P^{-1} \boldsymbol x_0 \end{split}\]

すなわち, 解の時間変化については, この部分に集約されている. さらに, \(J\) は \(A\) の対角化行列なので, \(A\) の固有値を対角に並べたものになっている. よく, 線形システムの挙動はその固有値によって決まる, と言われるが, それはこのような意味である [3].

実正方行列が対角化できない場合も, 定理 3.13 により, \(J_\mathrm c = P^{-1} A P\) と変形できて, \(\boldsymbol x(t) = Pe^{t J_\mathrm c} P^{-1} \boldsymbol x_0\) とできる. この場合も時間変化は \(e^{tJ_\mathrm c}\) の部分のみで定まる.

指数関数の挙動（1変数）

1変数の関数としての指数関数 \(y = e^{at}\) の挙動は, \(a>0\) の場合, \(x \to -\infty\) で \(e^{at} \to 0\) , \(x \to \infty\) で \(e^{at} \to \infty\) . \(a<0\) の場合 \(x \to-\infty\) で \(e^{at} \to \infty\) , \(x \to \infty\) で \(e^{at} \to 0\) となる.


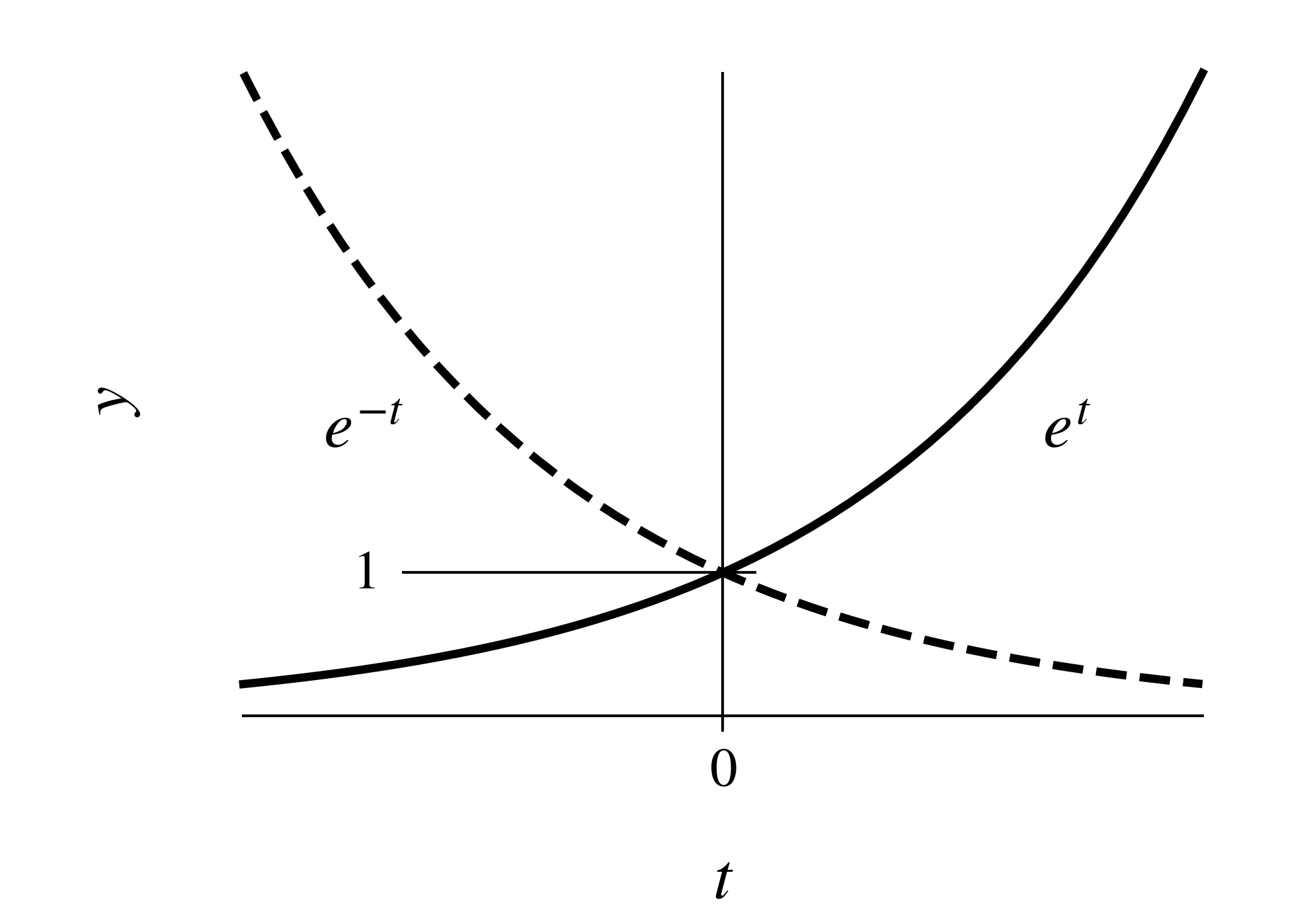
../_images/exponential_1d.png

図 9 指数関数 \(e^t\) と \(e^{-t} の挙動\)


言い換えれば, \(a < 0\) のとき \(x \to \infty\) で \(e^{ax}\) は \(0\) に収束するが, \(a> 0\) のときは, \(x \to \infty\) で \(e^{ax}\) は無限大に発散する. これを用いて, 連立線形微分方程式の解が, 時間とともに（\(t \to \infty\) ）\(\boldsymbol 0\) に収束するか発散するか, さらにはあるベクトルの方向に収束するか発散するかを判定できる.

行列 \(A\) が対角行列の場合

行列の指数関数 \(e^{tA}\) の 行列 \(A\) が対角行列の場合, 式 (26) がそのまま使える. \(e^{tJ}\) の各対角項は, \(t \to \infty\) のとき, \(d_i > 0\) ならば無限大に発散し, \(d_i <0\) ならば \(0\) に収束する.

例題 3.4

例題 3.1 の \(\boldsymbol x(t)\) は次のようなベクトルだった. \(\boldsymbol x(t)\) の \(t \to \infty\) での挙動はどうなるか.

\[\begin{split}\begin{split} \boldsymbol x(t) = \begin{bmatrix} \begin{array}{c} e^{-t} \\ e^{2t} \end{array} \end{bmatrix} \end{split}\end{split}\]

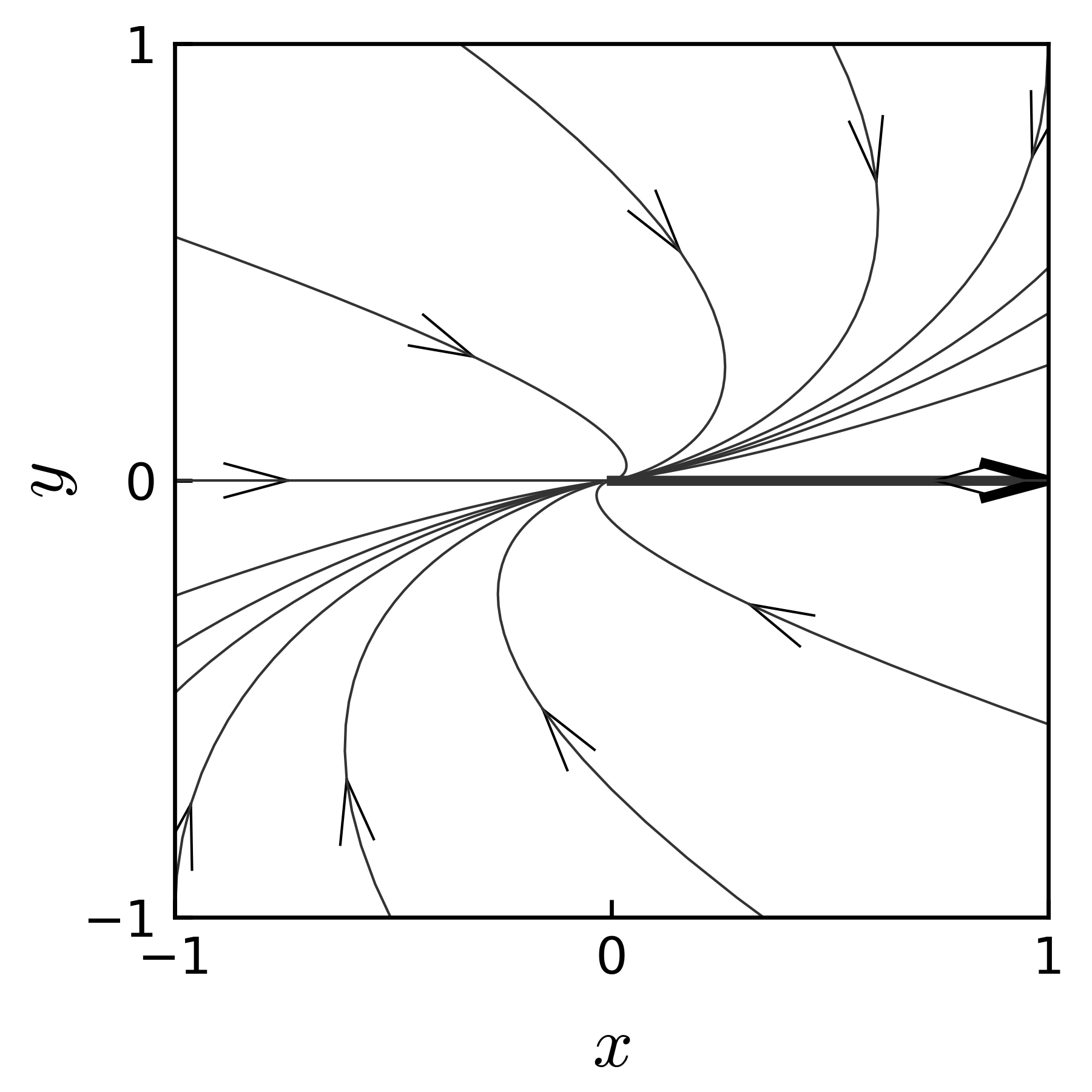
解答 例題 3.4 \(\boldsymbol x = [x, y]^\mathrm T\) とすると, \(t \to \infty\) のとき, \(x\to 0\) であり, \(y\) 軸の初期値 \(y_0\) が正 \((y_0 >0)\) のとき \(y \to \infty\) で, 負 \((y_0 < 0\) のとき, \(y \to - \infty\) である. \(y_0= 0\) のとき, すなわち初期値が \(x\) 軸上にある時, \(y\equiv 0\) であり,（\(t \to \infty\) に対して） \((x, 0) \to (0, 0)\) となる. 連立微分方程式の解をみるとき, 軌跡を図示すると挙動を把握しやすい. 図 10 に, この 例題 3.4 の様々な初期値に対する軌跡を示す. 解答にみるように, この微分方程式の解は \(y_0\) の正負に対応して, \(y \to \pm \infty\) に発散し, \(x\) 方向では \(0\) に近づく. \(y_0=0\) すなわち初期値が \(x\) 軸上にある場合は, \((x, y) \to (0, 0)\) に収束する.


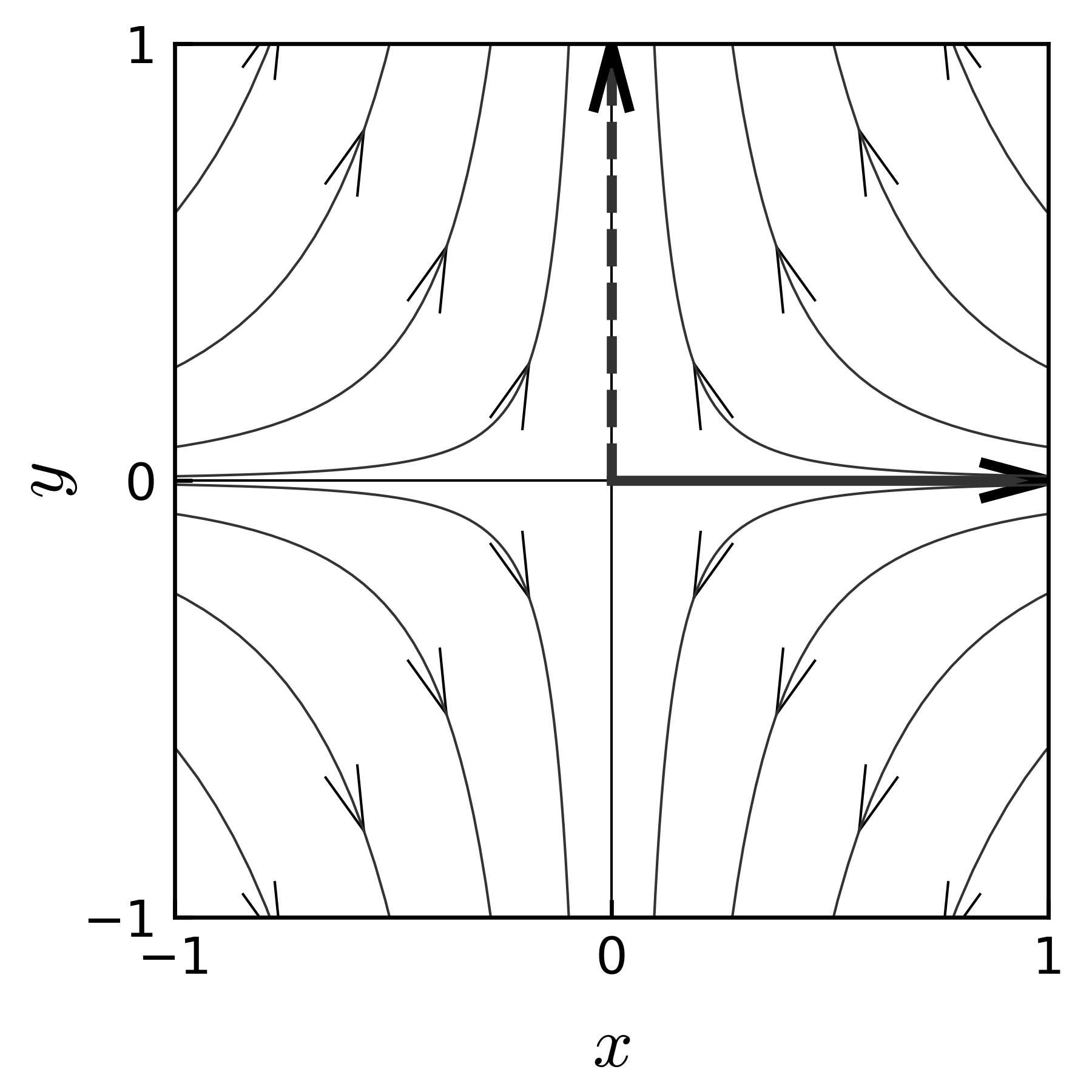
../_images/example_trajectories_diagonal_matrix_pm_sde.png

図 10 様々な初期値に対する軌跡（例題 3.4 ）


さて, 例題 3.1 , 例題 3.4 の微分方程式の行列 \(A\) の \(a_{11}\) 項の符号を変えた場合

(27)\[\begin{split}\frac{d \boldsymbol x}{dt} = A \boldsymbol x, \quad A = \begin{bmatrix} -1 & 0 \\ 0 & -2 \end{bmatrix}\end{split}\]

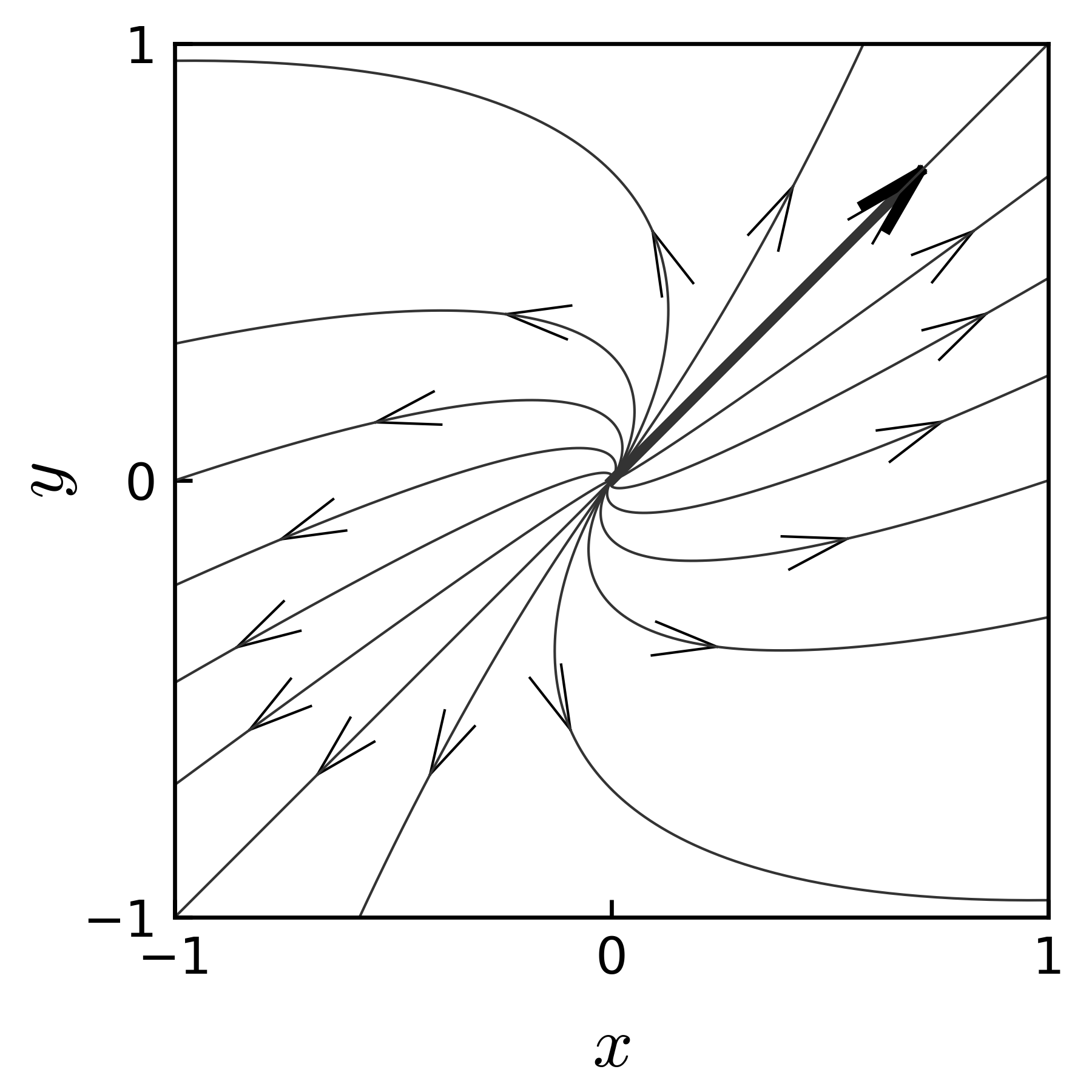
の様々な初期値に対する軌跡を 図 11 に示す. \(a_{11}\) 項の符号が変わるだけで, 軌跡の形が大きく変わることが分かる.


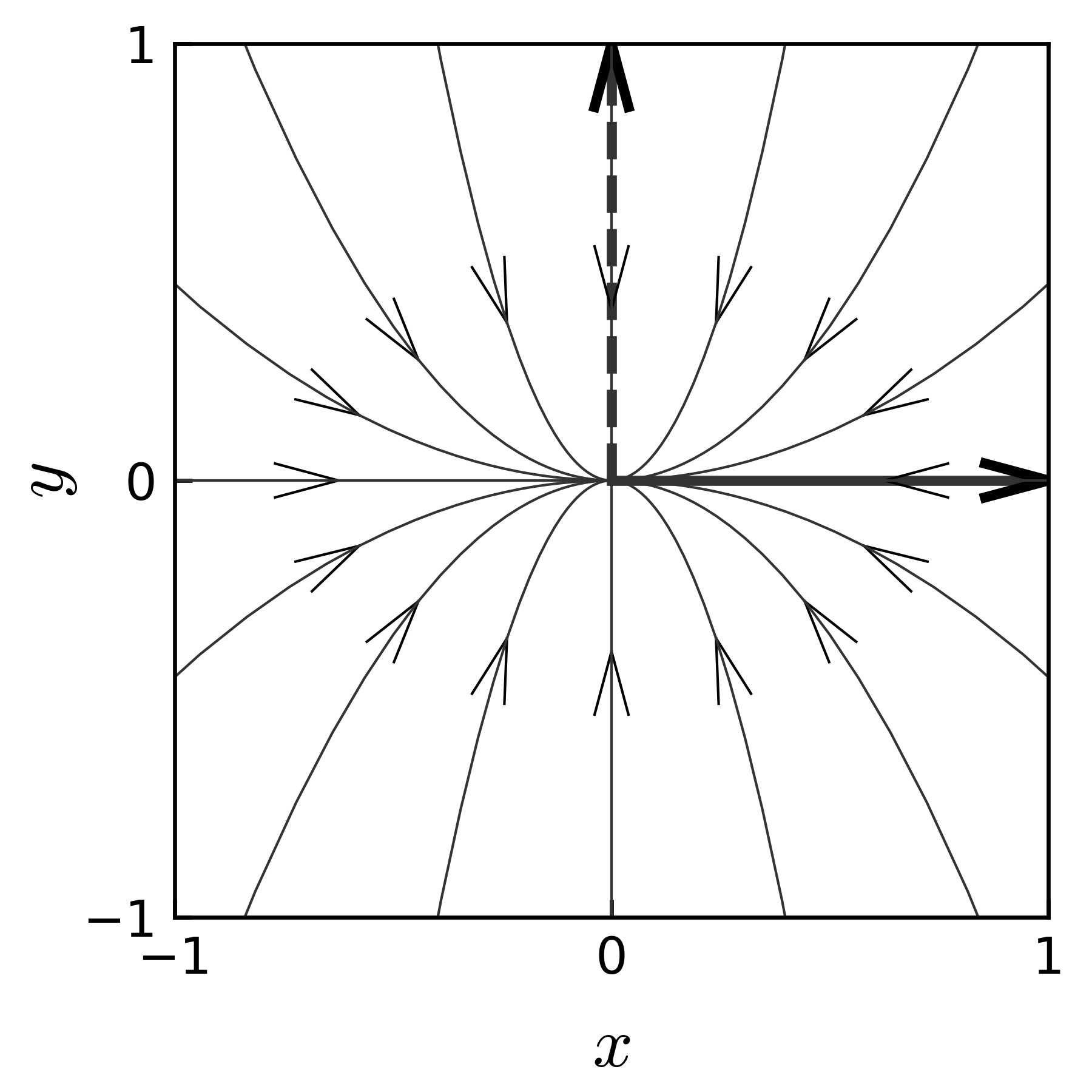
../_images/example_trajectories_diagonal_matrix_sde.png

図 11 初期値問題（式(27) ）の様々な初期値に対する軌跡


初期値問題 (27) の場合, 初期値にかかわらず \(t \to \infty\) に対して, \((x, y) \to (0, 0)\) に収束する.

上のふたつの例では, 初めから行列が対角になっている場合を示した. 次に, 一般の対角化行列で固有値がすべて実数の場合の例を示そう.

行列 \(A\) が対角化可能な場合

行列の指数関数 \(e^{tA}\) の 行列 \(A\) の固有値を \(\lambda_1, \dotsc, \lambda_n\) とすると, \(e^{tA}\) の対角化行列 \(e^{tJ}\) は, 第 \(i\) 成分が \(e^{t\lambda_i}\) の対角行列になる（式(26) ）.　この各対角項は, \(t \to \infty\) のとき, \(\lambda_i > 0\) ならば無限大に発散し, \(\lambda_i <0\) ならば \(0\) に収束する.

例題 3.5

\(\boldsymbol x_0\) に対して, \(A\) を対角化した行列を \(J\) とするとき, (1) \(e^{tJ}\) を求めよ. (2) \(t \to \infty\) で \(\boldsymbol x = e^{tA} \boldsymbol x_0\) はどうなるか.

\[\begin{split}\begin{split} A = \begin{bmatrix} \begin{array}{rr}-1.4 & 0.8 \\ 0.3 & -1.6 \end{array} \end{bmatrix}, \quad \boldsymbol x_0 \begin{bmatrix} \begin{array}{c} 1 \\ 1 \end{array} \end{bmatrix} \end{split}\end{split}\]

ただし, この行列 \(A\) の固有値（対角化行列 \(J\) の対角成分）は \(\lambda_1 = -1\) , \(\lambda_2 = -2\) となる.

解答 例題 3.5 (1) 固有値が \(-1\) , \(-2\) なので, 次式のようになる. (2) \(\boldsymbol x \to \boldsymbol 0 = \left[0, 0\right]^\mathrm T\) に収束する.

\[\begin{split}\begin{split} e^{tJ} = \begin{bmatrix} \begin{array}{cc} e^{-t} & 0 \\ 0 & e^{-2t} \end{array} \end{bmatrix} \end{split}\end{split}\]

解答はここまでとして, 参考までに \(e^{tA}\) を計算しておこう. 固有値 \(\lambda_1\) , \(\lambda_2\) にそれぞれに対応する固有ベクトル（規準化せず）は \(\boldsymbol p_1 = \left[2, 1\right]^\mathrm T\) , \(\boldsymbol p_2 = \left[4, -3\right]^\mathrm T\) だから, 固有値を並べた行列 \(P = \left[\boldsymbol p_1, \boldsymbol p_2 \right]\) とその逆行列 \(P^{-1}\) を用いて.

\[\begin{split}\begin{aligned} e^{tA} & = P e^{tJ} P^{-1} = \begin{bmatrix} \begin{array}{rr} 2 & 4 \\ 1 & -3 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{cc} e^{-t} & 0 \\ 0 & e^{-2t} \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{rr} 0.3 & 0.4 \\ 0.1 & - 0.2 \end{array} \end{bmatrix} \\ & %= \frac{1}{10}\begin{bmatrix} 2e^{-t} & 4e^{-2t} \\ e^{-t} & -3 e^{-2t} \end{bmatrix} %\begin{bmatrix} 3 & 4 \\ 1 & -2\end{bmatrix} = \frac{1}{10} \begin{bmatrix} \begin{array}{cc} 6e^{-t} + 4 e^{-2t} & 8e^{-t} - 8e^{-2t} \\ 3e^{-t} - 3 e^{-2t} & 4e^{-t} + 6e^{-2t} \end{array} \end{bmatrix}\end{aligned}\end{split}\]

となる.

計算が面倒なわりに, 出てきた答えを見ても, この解がどのような挙動をするかいまいちよく分からない. この式よりも,

\[\begin{split}\begin{split} \boldsymbol x (t) = P \begin{bmatrix} \begin{array}{cc} e^{-t} & 0 \\ 0 & e^{-2t} \end{array} \end{bmatrix} P^{-1} \boldsymbol x_0 \end{split}\end{split}\]

の形の式のほうが, 解の挙動の見通しが良い. この式で, \(P^{-1}\) は, 元の基底 \(\boldsymbol e_1 = \left[ 1, 0 \right]^\mathrm T\) , \(\boldsymbol e_2 = \left[ 0, 1 \right]^\mathrm T\) を, 固有ベクトルの基底 \(\boldsymbol p_1\) , \(\boldsymbol p_2\) に変換し, \(P\) は固有ベクトルの基底の基底を元の基底 \(\boldsymbol e_1\) , \(\boldsymbol e_2\) に変換している. \(P^{-1}\) と \(P\) は基底変換（座標変換）を行っているだけで, 先ほども述べたとおり, 系の時間変化はすべて \(e^{tJ}\) に含まれている.

これを図にすると, 図 12 のようになる. 図の一番下の矢印で, 初期値（初期条件）\(\boldsymbol x_0\) に対して, 微分方程式の演算子 \(e^{tA}\) が作用して, \(\boldsymbol x(t)\) になると考える. 次に, \(\boldsymbol x_0\) の固有ベクトル \(\boldsymbol p_1\) , \(\boldsymbol p_2\) の基底のもとでの座標を \(\boldsymbol \xi_0\) とする. これは, \(\boldsymbol x_0\) に行列（線形変換）\(P^{-1}\) を作用させることで, \(\boldsymbol \xi_0 = P^{-1} \boldsymbol x_0\) として求まる. 固有ベクトルの座標では, 時間 \(t\) 経過後の値 \(\boldsymbol \xi(t)\) は, この \(\boldsymbol \xi_0\) に \(e^{tJ}\) が作用して, \(\boldsymbol \xi(t) = e^{tJ} \boldsymbol \xi_0\) として求まる. これを \(P\) で元の座標系に戻して, \(\boldsymbol x(t) = P \boldsymbol \xi(t)\) を得る.


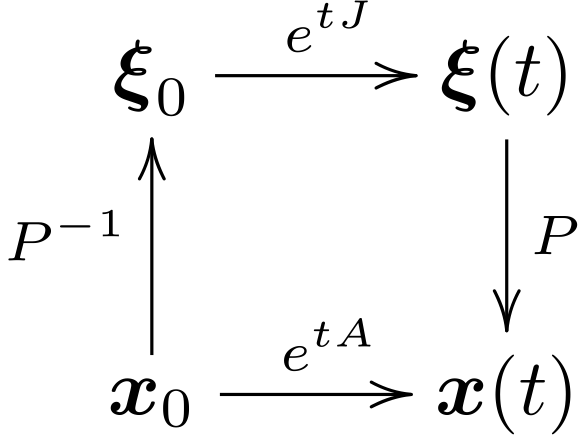
../_images/figetAetJ.png

図 12 行列の指数関数の座標変換


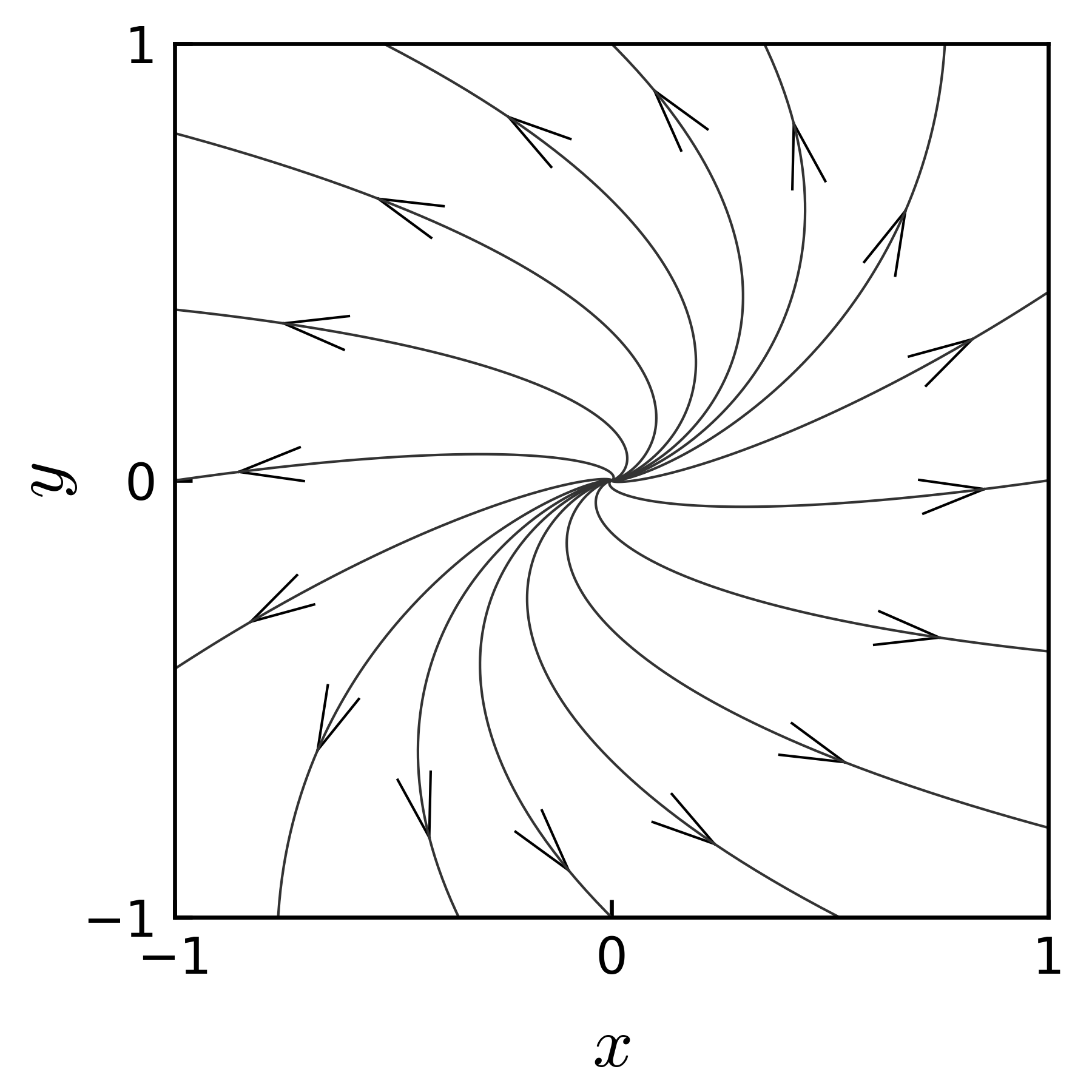
このようにすると, 座標変換, 時間による変化, 座標変換（元に戻す）, という操作で, 解の挙動の見通しが良くなることが分かる.


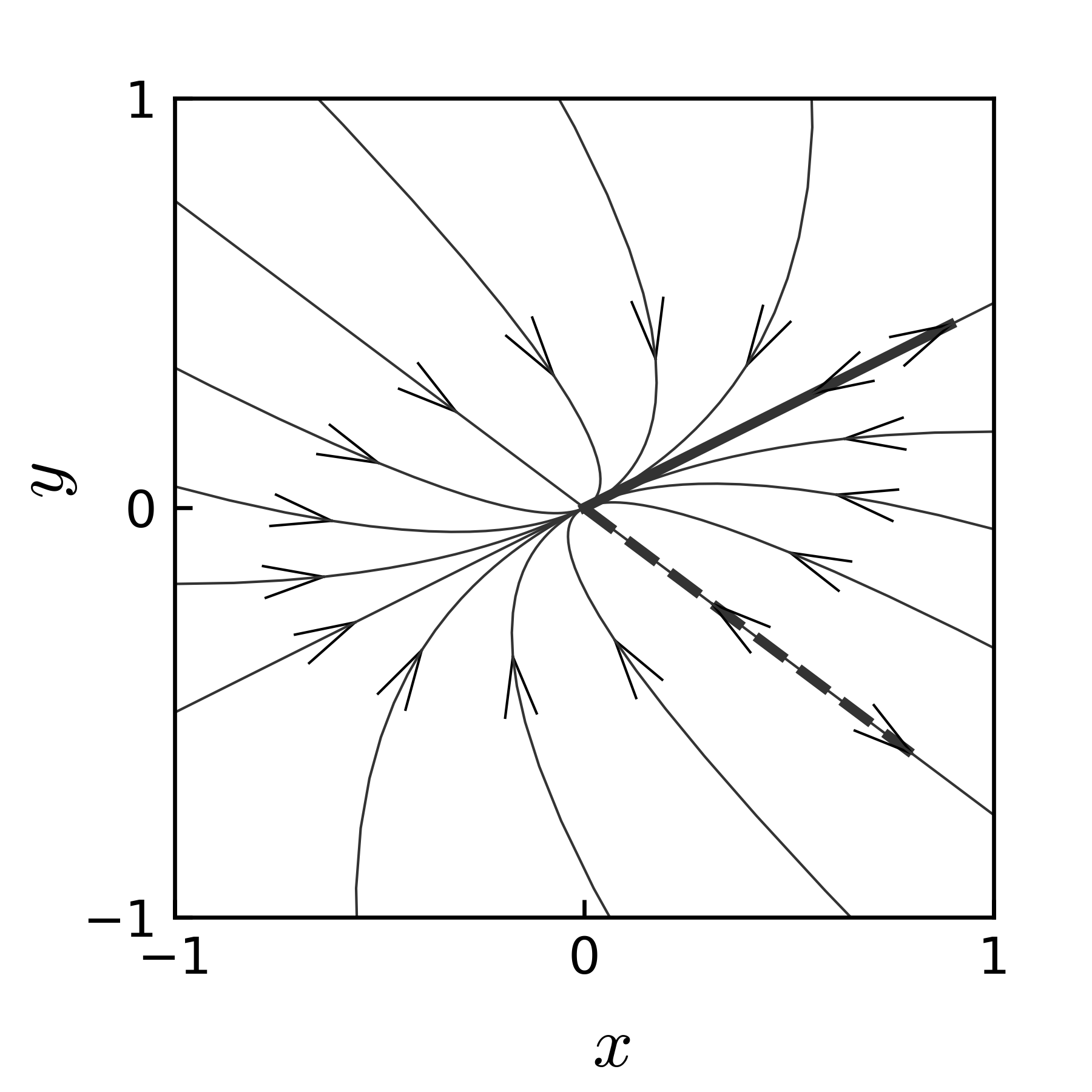
../_images/example_trajectories_eta_01.png

図 13 例題 3.5 の 解のさまざまな初期値に対する軌跡, 太い線の矢印は, 固有べクトル



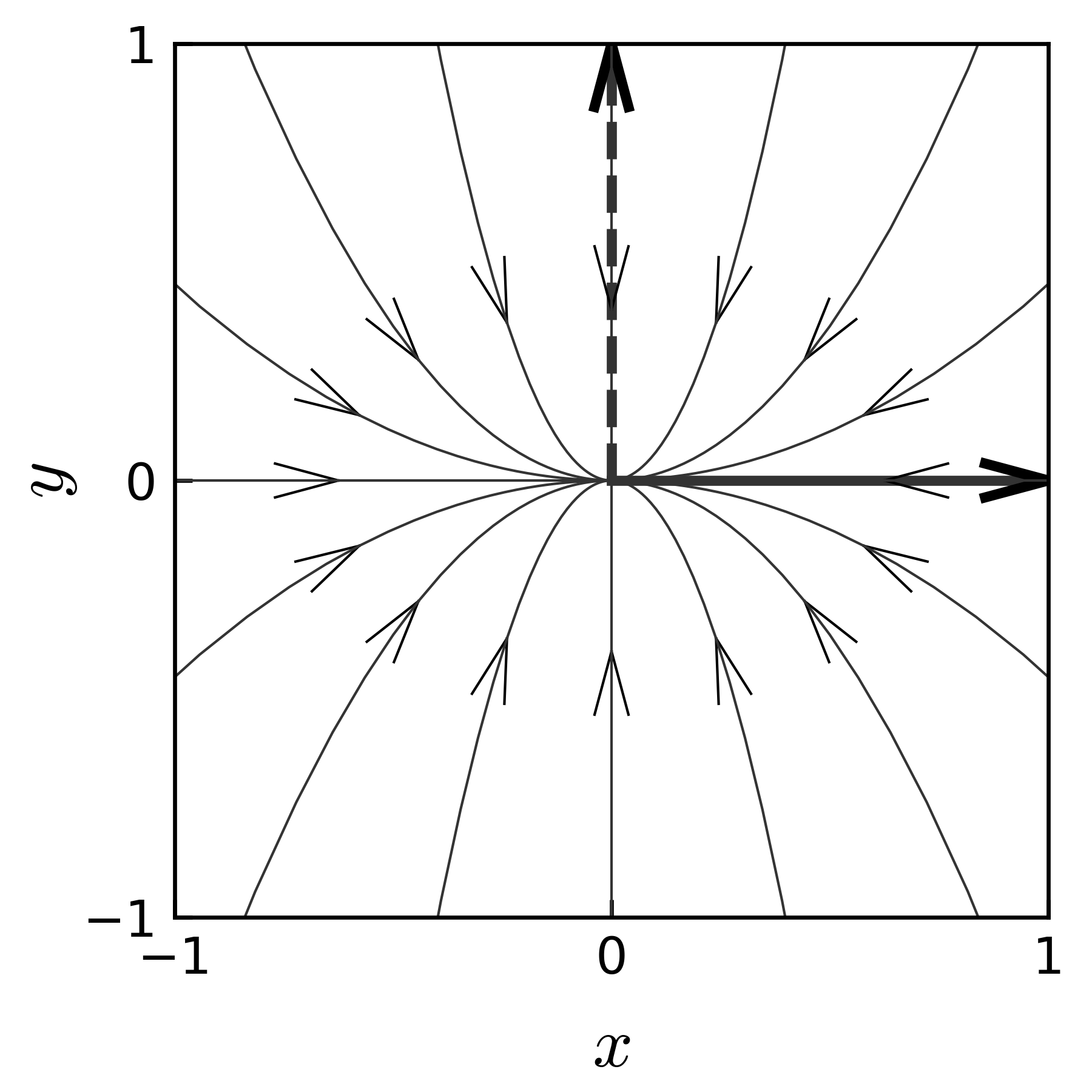
../_images/example_trajectories_etj_01.png

図 14 例題 3.5 の \(e^{tJ} \boldsymbol \xi_0\) の固有ベクトル基底における座標 \(\left( \xi_1, \xi_2 \right)\) での様々な \(\boldsymbol \xi_0\) に対する軌跡, 太い線の矢印は, この座標系における単位ベクトル \(\boldsymbol e_{\xi 1}\) （実線）, \(\boldsymbol e_{\xi 2}\) （破線）


図 13 に, \(xy\) 平面でのこの微分方程式の様々な初期値に対する解の軌跡を示す. また, 図 14 に, 固有ベクトルの座標系での解の軌跡を示す.

図 14 の軌跡は, 例題 3.4 の場合の 図 11 と, 座標が違う（前者が固有ベクトルの座標, 後者は \(xy\) 座標）だけで, 全く同じになる. すなわち, 例題 3.5 において, 解の時間変動の本質的な部分は, 対角化された \(J\) を用いた \(e^{tJ}\) に含まれており, \(P\) と \(P^{-1}\) は座標変換のみを行っていることが, 図からも了解される.

解の挙動のうち, \(\boldsymbol x \to \boldsymbol 0\) となる場合は, システムの安定性等において重要な役割を果たす. これを命題としてまとめておく.

命題 3.14

連立微分方程式の初期値問題 (18) において, 行列 \(A\) が対角化可能な場合, 固有値が全て負である場合, \(t \to \infty\) のとき \(\boldsymbol x \to \boldsymbol 0\) に収束する.

行列が対角化できない場合

この場合, Jordan 細胞を含む形にしか変形できない. まずは 行列が jordan 細胞の形をしている場合を考えよう.

例 3.15

\[\begin{split}\begin{split} A = \begin{bmatrix} -1 & 1 \\ 0 & -1 \end{bmatrix} \end{split}\end{split}\]

この 2 次の Jordan 細胞 に対する \(e^{tA}\) の様々な初期値に対する軌跡を, 図 15 に示す.


../_images/example_trajectories_degenerated_jordan_cell.png

図 15 2 次の Jordan 細胞, 固有ベクトルは \(\boldsymbol e_1\) ひとつ


例 3.16

一般の縮退行列の例として, 次の行列 \(A\) を考え, \(e^{tA}\) の軌跡をみる.

\[\begin{split}\begin{split} A = \begin{bmatrix} 3 & -1 \\ 1 & 1 \end{bmatrix} \end{split}\end{split}\]

../_images/example_trajectories_degenerated.png

図 16 縮退行列の例, 固有ベクトルはひとつ


備考 3.17

以上2つの 例 3.15 では \(\boldsymbol p = \left[1, 0\right]^\mathrm T\) , 例 3.16 では \(\boldsymbol p = \left[1/\sqrt 2 , 1 / \sqrt 2 \right]^\mathrm T\) ）. 例 3.15 , 例 3.16 の固有値はそれぞれ \(-1\) , \(2\) なので, \(t \to \infty\) で軌跡は 前者では \(\boldsymbol x = \boldsymbol 0\) に収束し, 後者では発散する. 収束するときに, 最終的には固有ベクトル方向に漸近しながら \(\boldsymbol x = \boldsymbol 0\) に近づく. この場合も収束・発散は固有値によってのみ決まる.

命題 3.18

連立微分方程式の初期値問題 (18) において, 行列 \(A\) の固有値がすべて実数であるが, 対角化できずに, Jordan 細胞を含む形にしか変形できない場合においても, 固有値が全て負である場合, \(t \to \infty\) のとき \(\boldsymbol x \to \boldsymbol 0\) に収束する.

固有値が共役複素数の場合の解の挙動

基礎知識

固有値が共役複素数を表す行列の図形への作用は回転を含む. よって, このような行列 \(A\) に対する微分方程式の初期値問題(18) の解は何らかの回転を含む. このとき, 固有値が純虚数であれば, 解の軌跡は円となる. それ以外の場合は, 固有値の実部が正であれば, \(t \to \infty\) の時 \(\boldsymbol x\) は発散, 固有値の実部が負であれば \(\boldsymbol x = \boldsymbol 0\) に収束する.

回転を表す行列・一般形

前章で論じたように, 行列

(28)\[\begin{split}\begin{split} A = \begin{bmatrix} \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \end{bmatrix} \end{split}\end{split}\]

は, 図形に対して, 反時計回りの角度 \(\theta\) だけの回転の作用をする. さて, この固有値であるが, 固有方程式が

\[\begin{split} \lambda - 2 \cos \theta + 1 = 0 \end{split}\]

であるから, 固有値が

\[\begin{split} \lambda = \cos \theta \pm \sqrt{ \cos^2 \theta - 1} = \cos \theta \pm i \sin \theta \end{split}\]

である. 初期値問題(18) の解の挙動は, この固有値によって決まる.

図 17 に, \(\theta\) が \(\pi/4\) , \(\pi/2\) , \(3\pi/4\) の場合の解の挙動を示す. それぞれの場合に実部は \(1 / \sqrt 2\) , \(0\) , \(- 1 / \sqrt 2\) だが, この実部の正, \(0\) , 負に対応して, 解の軌跡は発散, 円, 収束, となっている. いずれの場合も回転角は \(0 < \theta < \pi\) なので, 反時計回りの回転が図に見られる.


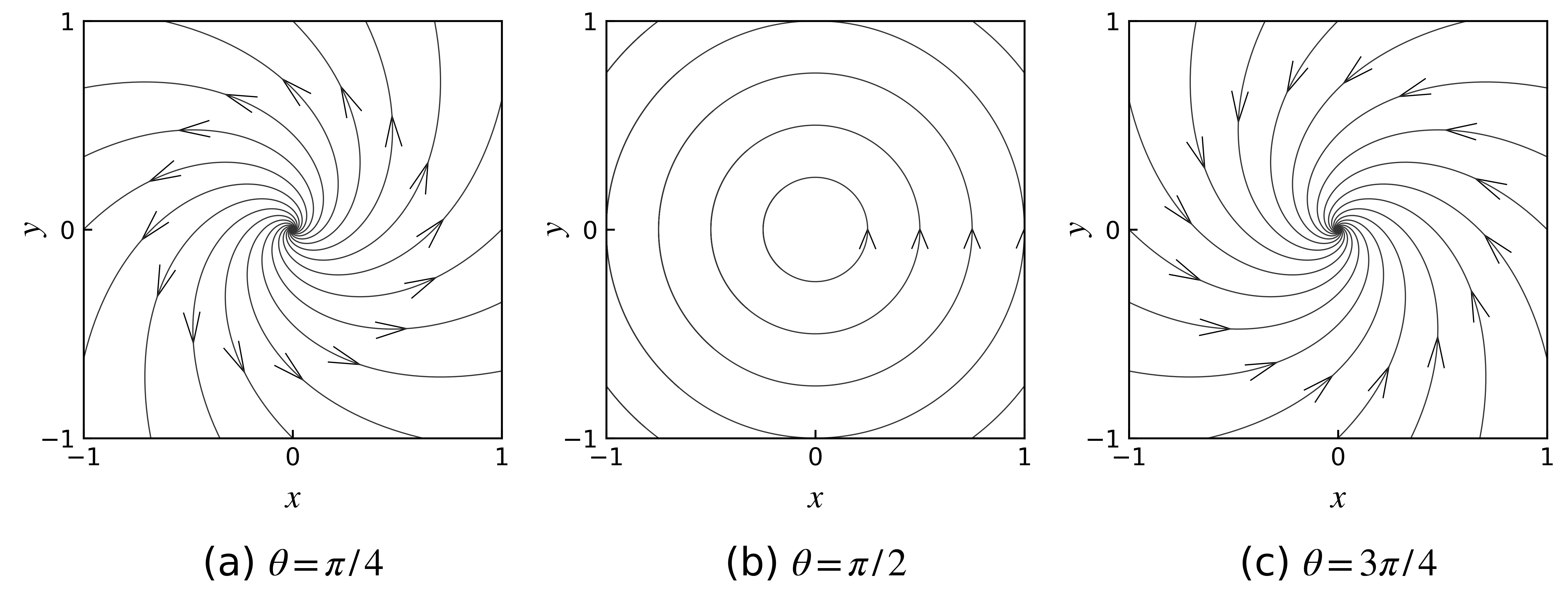
../_images/example_trajectories_rotation_summary_larger.png

図 17 回転を表す行列の場合の様々な初期値に対する解の軌跡


回転と拡大, 縮小を表す行列の場合

(29)\[\begin{split}\begin{split} A = a \begin{bmatrix} \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \end{bmatrix}, \quad a \ne 0, 1 \end{split}\end{split}\]

行列がこの式 (29) の形をしている場合, 初期値問題 (18) の解は, 式(28) における \(t\) が \(ta\) になるだけで, まったく同じ軌跡となる.

一般の共役複素数固有値

例 3.19

\[\begin{split}\begin{aligned} A = \begin{bmatrix} \begin{array}{rr} 7/8 & -5/8 \\ 1/8 & 5/8 \end{array} \end{bmatrix}\end{aligned}\end{split}\]

の固有値は \(\lambda = 3/4 \pm i/4\) である. 解の挙動は次のようになる.


../_images/example_trajectories_conjugate_eigenvalues.png

図 18 共役複素数の固有値をもつ行列による連立微分方程式の様々な初期値に対する軌跡


この場合の軌跡は 図 18 のように, 図 17 (a) のグラフ少し変形した形になる. 固有値の実部が \(3/4\) で正なので, \(t \to \infty\) で発散する. 固有値が共役複素数の場合は, このように, 実部の政府で発散・収束が決まってくる.

命題 3.20

連立微分方程式の初期値問題 (18) において, 行列 \(A\) が共役複素数をもつ場合, その実部が全て負であれば, \(t \to \infty\) のとき \(\boldsymbol x \to \boldsymbol 0\) に収束する.

解の挙動のまとめ

収束する場合

前節で様々な場合における収束の条件をみてきたが, これらをまとめて次が言える.

定理 3.21

連立微分方程式の初期値問題 (18) において, 行列 \(A\) の固有値の実部が全て負であれば, \(t \to \infty\) のとき \(\boldsymbol x \to \boldsymbol 0\) に収束する.

場合分け

さて, \(2 \times 2\) 実正方行列は, 固有値が実数の場合と共役複素数のペアの場合に分けられる. さらに, 前者は, 対角化できる場合と, 2 次の Jordan 細胞 の形に標準化できる場合に分けられる. よって, ここでは, (1) 対角化できて固有値が実数の場合, (2) 2 次の Jordan 細胞 に標準化できる場合, (3) 固有値が共役複素数の場合, に分けて整理する.

行列が対角化可能で固有値が実数の場合

この場合行列は適当な座標変換で対角行列になる. 対角化行列の挙動の分類のために, 次の形の行列を考える.

(30)\[\begin{split}\begin{split} A = \begin{bmatrix} \begin{array}{rr} a & 0 \\ 0 & -1 \end{array} \end{bmatrix} \end{split}\end{split}\]

この行列の挙動が \(a\) の値によってどのように変化するかを見てみよう（ 図 19 ）.

  1. \(\ a < -1\) の場合: \(\lvert a \rvert\) は, 右下の対角要素 \(-1\) よりも大きいので, \(x\) 方向のほうが \(y\) 方向よりも速く小さくなる. よって, 軌跡は \(x\) 軸を軸とする放物線状になる.

  2. \(\ a = -1\) の場合: 対角成分がともに \(-1\) で等しいので, \(x\) 方向と \(y\) 方向で同じ速さで変化する. よって, 軌跡は初期値からまっすぐに原点をめざす形になる.

  3. \(\ -1 < a < 0\) の場合: \(\lvert a \rvert < \lvert -1 \rvert\) なので, \(y\) 方向のほうが \(x\) 方向より速く小さくなる.

  4. \(\ a=0\) の場合: \(x\) 方向の変化はなく, \(y\) 方向にのみ変化する. \(t \to \infty\) で, \(y \to 0\) となる.

  5. \(\ a > 0\) の場合: もう一方の対角成分は \(-1\) なので, \(t \to \infty\) で \(x\) 方向は無限大に発散, \(y\) 方向は \(0\) に収束する.


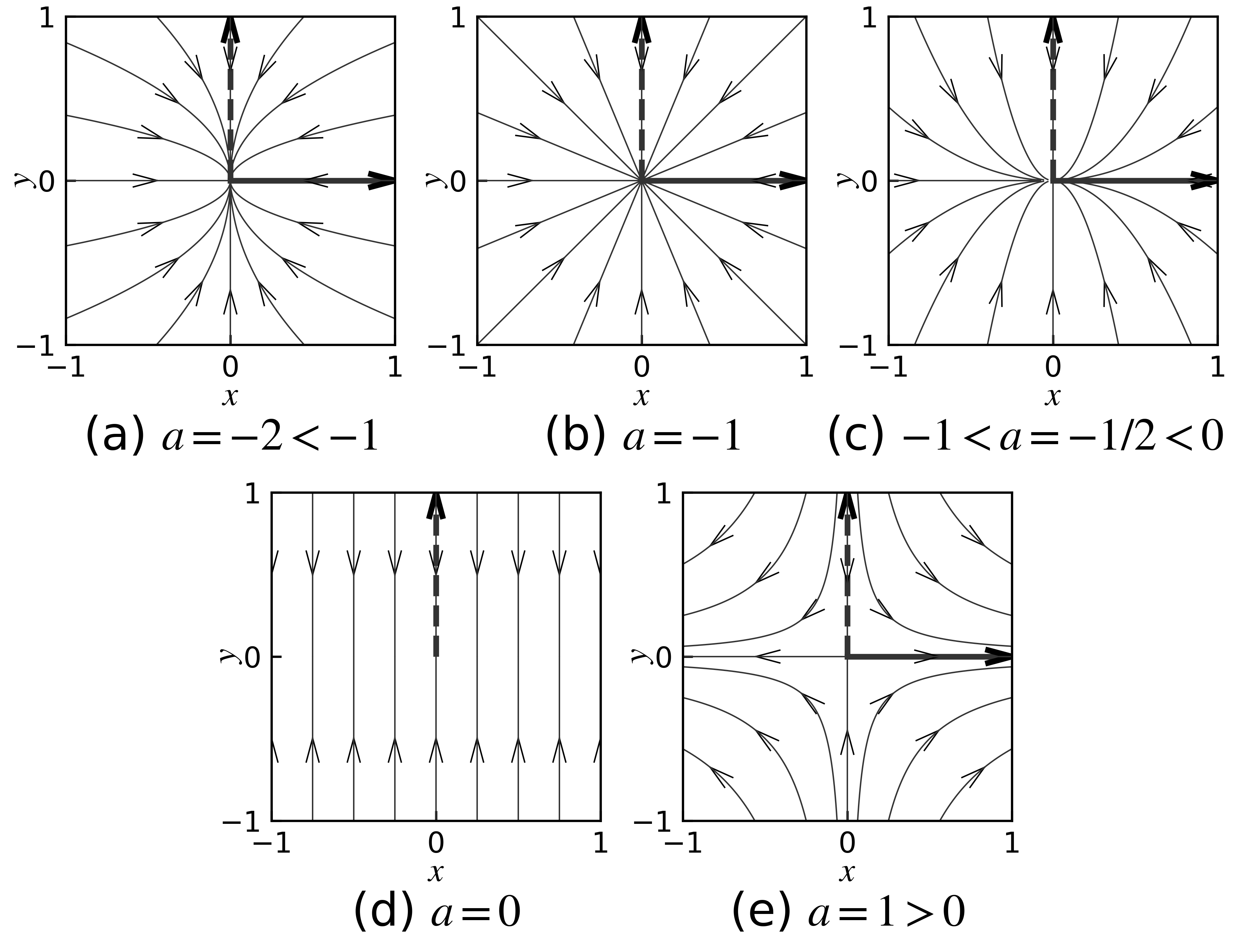
../_images/various_diagonizable.png

図 19 対角化可能行列の \(e^{tJ}\) の挙動


さて, 式 (30) の右下の項 \(a_{22}=-1\) の符号を変えた行列

\[\begin{split}\begin{split} B = \begin{bmatrix} \begin{array}{rr} b & 0 \\ 0 & 1 \end{array} \end{bmatrix} \end{split}\end{split}\]

について考える. この場合の \(e^{tB}\) については, (a) \(b > 1\) のとき, 図 19 (a) の変化の向きが逆になった場合, (b) \(b=1\) のとき, 図 19 (b) の逆向き, (c) \(0 < b < 1\) のとき, 図 19 (c) の逆向き, (d) \(b=0\) のとき, 図 19 (d) の逆向き, (e) \(b<0\) のとき, 図 19 (e) の逆向き, となる.

固有値が実数で行列が対角化できない場合の解の挙動

\(2 \times 2\) 行列の固有値がすべて実数で対角化できない場合, すなわち, 固有値が縮退している場合, 適当な基底変換により, 次の形の行列となる.

\[\begin{split}\begin{split} A = \begin{bmatrix} \begin{array}{cc} a & 1 \\ 0 & a \end{array} \end{bmatrix} \end{split}\end{split}\]

このとき, \(e^{tA}\) は, \(a\) の正負により発散か収束かが決まる.


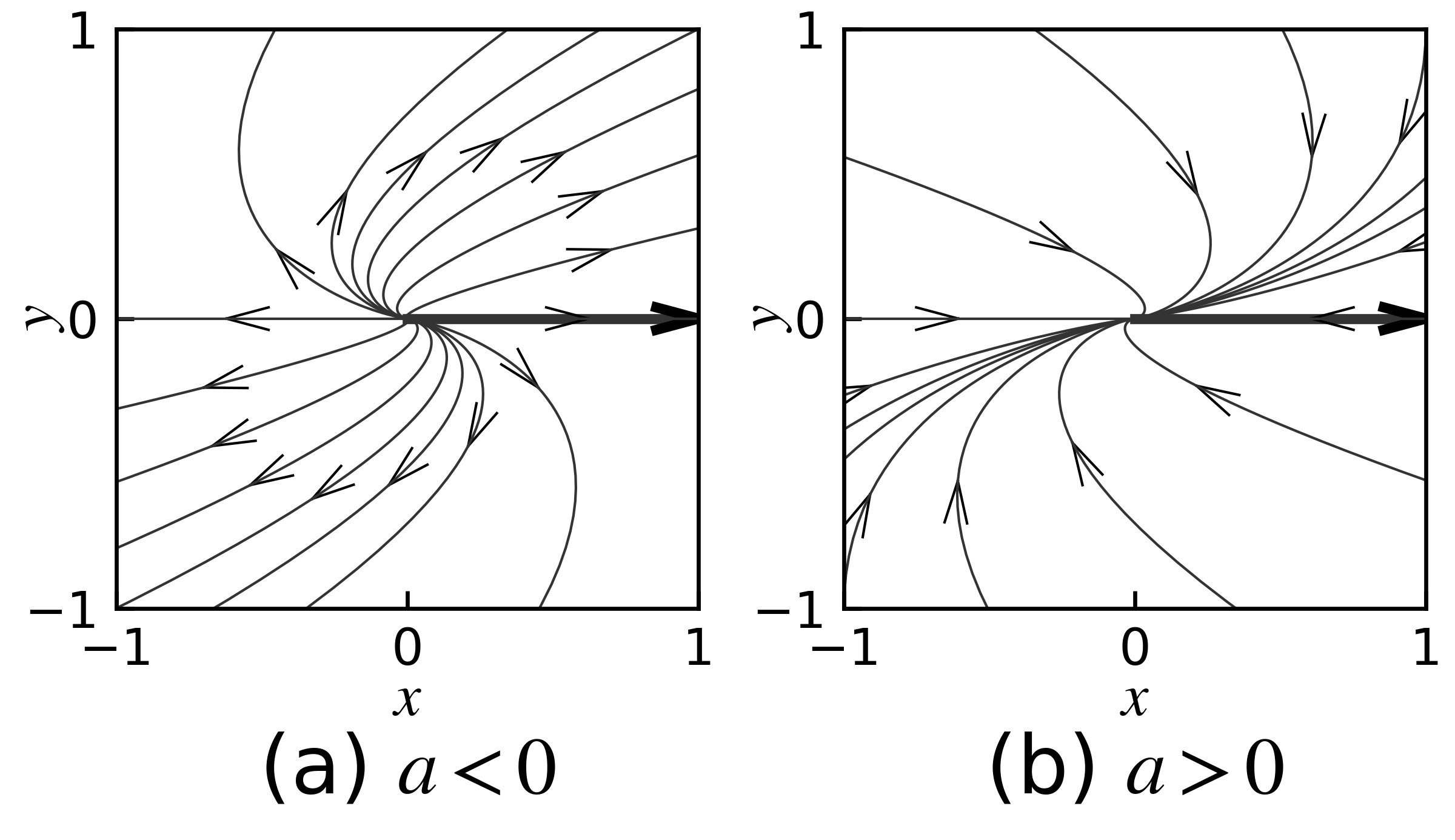
../_images/example_trajectories_jordan_cell_summary.png

図 20 縮退行列の解の挙動


固有値が共役複素数の場合の解の挙動

固有値が共役複素数の場合は, 固有値の実部の正負によって発散か収束かが決まる.


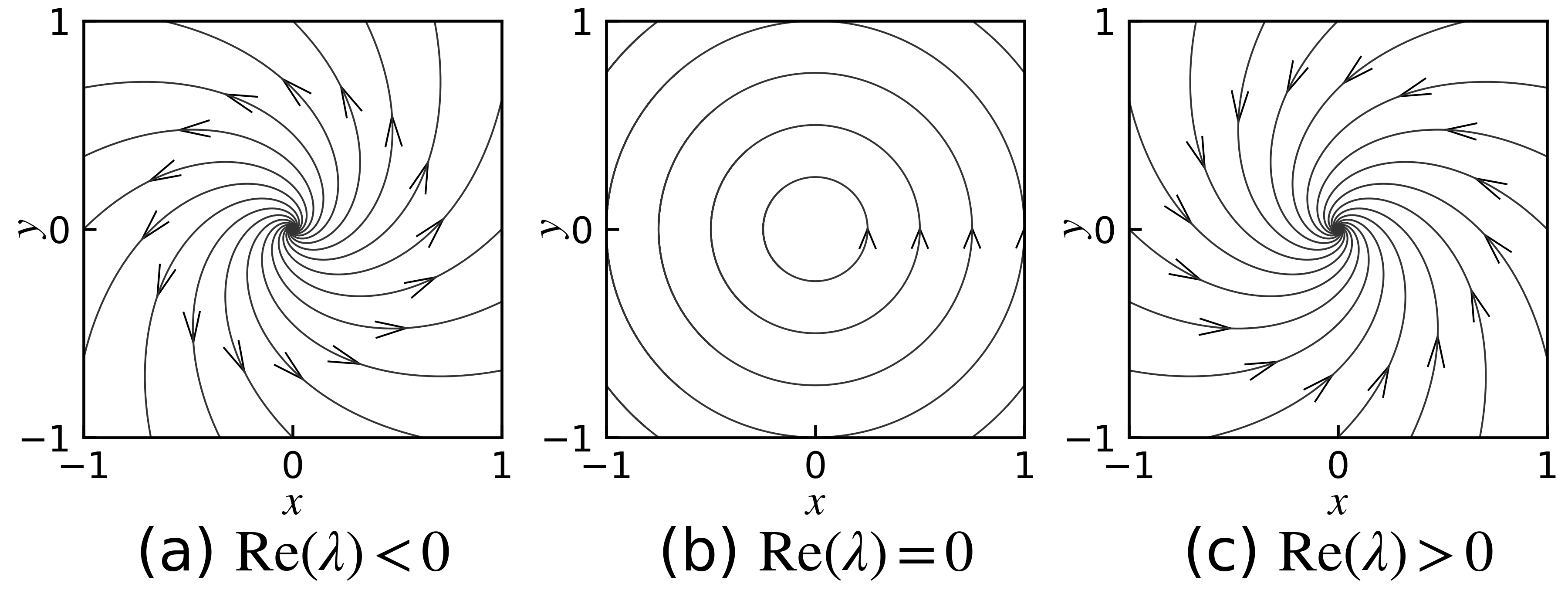
../_images/example_trajectories_rotation_summary.png

図 21 固有値が共役複素数となる場合の解の挙動


まとめの例題

例題 3.6

座標変換の作用を除けば, 図 19 の (a) から (e) のうちのどれに最も近くなるか. ただし, 解の向き（収束か発散か）は問わず, (a) と (c) は区別しないとする.

\[\begin{split}\begin{split} & (1) \quad A = \begin{bmatrix} \begin{array}{rr} 1 & 2 \\ 3 & 4 \end{array} \end{bmatrix}, \quad (2) \quad A = \begin{bmatrix} \begin{array}{rr} 1 & -2 \\ 3 & -4 \end{array} \end{bmatrix} \end{split}\end{split}\]

解答例題 3.6 (1) 固有方程式は \(\lambda^2 - 5 \lambda -2 = 0\) より, \(\lambda = 5/2 \pm \sqrt{33}/2\) より, \(\lambda = -0.3723, 5.3723\) . 一方が正でもう一方が負なので, 図 19 の (e) に最も近い. (2) 固有方程式は \(\lambda^2 - 3 \lambda + 2 = 0\) より \(\lambda =-1, -2\) ともに負で異なる値なので, 図 19 の (a) （あるいは (c) ）に最も近い.

参考書

講義内容の理解のためには, 次の小寺の 4 章が良い.

線形微分方程式系から力学系, カオスへは例えば,

演習問題

問題 3.1

\(x = f(t) = e^{-kt}\) を \(t=0\) の周りで \(t\) の 3 次の項まで Taylor 展開せよ. ただし, 剰余項はただ \(R\) と示すのみでよい.

問題 3.2

次の微分方程式を初期値問題を解け.

\[\frac{d x}{d t } = - k x, \quad x(0) = 1\]

問題 3.3

次の微分方程式を, 下に示す行列と初期条件のもとで解け.

\[\begin{split}\frac{d \boldsymbol x}{d t} = A \boldsymbol x, \quad A = \begin{bmatrix} \begin{array}{rr} 3 & 0 \\ 0 & -1 \end{array}\end{bmatrix}, \quad \boldsymbol x_0 = \begin{bmatrix} 1 \\ 1 \end{bmatrix}\end{split}\]

問題 3.4

行列 \(A\) は次のように対角化される.

\[\begin{split}\begin{aligned} A &= \begin{bmatrix} \begin{array}{rr} - \frac{3}{8} & - \frac{1}{8} \\ - \frac{1}{8}& - \frac{-3}{8} \end{array} \end{bmatrix} = PJP^{-1} \\ & = \begin{bmatrix} \begin{array}{rr} \frac{\sqrt 2}{2} & - \frac{\sqrt 2}{2} \\ \frac{\sqrt 2}{2} & \frac{\sqrt 2}{2} \end{array} \end{bmatrix}\begin{bmatrix} \begin{array}{rr} -\frac{1}{2} & 0 \\ 0 & - \frac{1}{4} \end{array}\end{bmatrix} \begin{bmatrix}\begin{array}{rr} \frac{\sqrt 2}{2} & \frac{\sqrt 2}{2} \\ - \frac{\sqrt 2}{2} & \frac{\sqrt 2}{2} \end{array}\end{bmatrix}\end{aligned}\end{split}\]

\(e^{tA}\) を求めよ.

問題 3.5

連立微分方程式 (18) の行列が次であるとき, 適当な座標変換後の軌跡の形はそれぞれ 図 19 の (a)〜(e) のどれに最も近くなるか. ただし, 軌跡の向き（収束か発散か）は問わないとし, (a) と (c) は区別しないとする.

\[\begin{split}\begin{aligned} & (1) \quad A = \begin{bmatrix}\begin{array}{rr} 2 & 1 \\ 1 & 2 \end{array}\end{bmatrix}, \quad (2) \quad A = \begin{bmatrix}\begin{array}{rr} 1 & -1 \\ -1 & 1 \end{array}\end{bmatrix}, \\ & (3) \quad A = \begin{bmatrix}\begin{array}{rr} 2 & 1 \\ 2 & 3 \end{array}\end{bmatrix}, \quad (4) \quad A = \begin{bmatrix}\begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array}\end{bmatrix}\end{aligned}\end{split}\]

問題 3.6

連立微分方程式 (18) の行列が次であるとき, 適当な座標変換後の軌跡の形は 図 21 の (a)〜(c) のどれに最も近くなるか. ただし, 渦巻きが左回りか右回りかは問わないとする.

\[\begin{split}\begin{aligned} &(1) \quad A = \begin{bmatrix} \begin{array}{rr} 4 & - 6 \\ 6 & 4 \end{array} \end{bmatrix}, \quad (2) \quad A = \begin{bmatrix} \begin{array}{rr} -2 & -4 \\ 3 & -1 \end{array} \end{bmatrix} \\ &(3) \quad A = \begin{bmatrix} \begin{array}{rr} 0 & 2 \\ -2 & 0 \end{array} \end{bmatrix}, \quad (4) \quad A = \begin{bmatrix} \begin{array}{rr} 0 & 2 \\ -1 & 0 \end{array} \end{bmatrix}\end{aligned}\end{split}\]

問題 3.7

連立微分方程式 (18) の行列が次であるとき, 適当な座標変換後の軌跡の形は, 図 19 (a)〜(e), 図 12 (a), (b), 図 21 (a) 〜 (c) のどれに最も近くなるか. ただし, 図 19 では, 軌跡の向き（収束か発散か）は問わず, (a) と (c) は区別しないとし, 図 21 では, 渦巻きが左回りか右回りかは区別しないとする.

\[\begin{split}\begin{aligned} &(1) \quad A = \begin{bmatrix} \begin{array}{rr} 0 & -1 \\ -1 & 0 \end{array} \end{bmatrix}, \quad (2) \quad A = \begin{bmatrix} \begin{array}{rr} 0 & 1 \\ -1 & 0 \end{array} \end{bmatrix}\end{aligned}\end{split}\]

◀ Previous TOC Next ▶