| ◀ Previous | TOC | Next ▶ |
2. 液体表面
2.1 液体表面の微視的描像
界面の厚さ
界面の厚さ
水の密度で見た場合, \(1 \ \mathrm{nm}\) のオーダー
イオン濃度で見た場合, デバイ長(第 4 章), 水中でのデバイ長 \(< 680 \ \mathrm{nm}\)
液体表面は, とても乱れのある場所
蒸発, 凝集, バルク中にある分子と表面にある分子の間の拡散など
具体例 2.1
\(1\) 分子の水の面積は \(10 ~ \mathrm{\mathring{A}}\), \(\displaystyle {k_{\mathrm B}=1.380649\times10^{-23}{\mathrm{J~K^{-1}}}}\), \(m=3\)\(\times10^{-26}~\mathrm{kg}\), \(T=298~{\mathrm K}\), \(P=3168~\mathrm{Pa}\), \(A=10\times10^{-20}~\mathrm{m^2}\)
面積 \(A\) の穴からの理想気体の流出速度 分子の個数/s は,
\begin{align*} v & = \frac{PA}{\sqrt{2\pi m k_\mathrm B T}} \quad \mathrm{[s^{-1}]} \tag{2.1} \end{align*}
25°C, の水の表面を考える.
表面近くの気相中の水蒸気分圧は飽和蒸気圧 \(P=3168 \ \mathrm{Pa}\) であると仮定できるとする.
\(10 \, \mathrm{\mathring{A}}^2\) の面積あたり, \(1\) 秒間に何個の水分子がぶつかるか.
ある分子が表面にとどまる平均時間を求めよ. \(1\) 水分子が占める水の面積は, 約 \(10 \, \mathrm{\mathring{A}}^2\) とする.
解答例 2.1
\begin{align*} v & = \frac{PA}{\sqrt{2\pi m k_\mathrm B T}} \quad \mathrm{[s^{-1}]} \\ & = \frac{(3168)(10 \times 10^{-20})} {\sqrt{(2)(3.145)(3 \times 10^{-26})(1.380649 \times 10^{-23})(298) }} \\ & = 1.1375876 \times 10^7 = 1.14 \times 10^7 \ \mathrm{s^{-1}} \end{align*}
約 \(1 \times 10^7 \ \mathrm{s^{-1}}\)
約 \(1\) \(\times\) \(10^{-7}\) \(\mathrm{s}\)
2.2 表面張力
表面張力と仕事
式 (2.2) は表面張力 \(\gamma\) の定義式.
仕事 \(\mathrm d W\) は表面積変化 \(\mathrm d A\) に比例する. 係数が表面張力.
表面張力は, 液体および気体の成分, 温度, 圧力に依存するが, 面積には独立である.
次元
\[\textsf{界面張力} = \frac{\textsf{仕事}}{\textsf{面積}} = \frac{\textsf{力}}{\textsf{長さ}}\]cf. 圧力, 応力: 力 / 面積
幅 \(b\) の液膜を引き伸ばすときの力
この 2 は, 膜の両面に表面ができることによる.
水の表面張力 25°C で \(72 \ \mathrm{mN~m^{-1}}\)
式 (2.2) と (2.3) は, 可逆変化では等価
膜を引っ張ると縮む方向に力が働くので, 式は負の符号を含む.
表面張力の温度依存性
ある温度 \(T_0\) での表面張力 \(\gamma(T_0)\) がわかっている場合,
これは次の式について Taylor の定理を使って 1 次までの近似をとったものである.
具体例 2.2
長さ 1 cm のスライド棒でフレームに水の液膜を作成する場合, この膜がスライド棒を引っ張る力を求めよ.
解答例 2.2
\begin{align*} F & = - \frac{\mathrm d W }{\mathrm d x} = -2 \gamma b \\ \lvert F \rvert & = (2)(72 \times 10^{-3})(0.01) \\ & = 1.44 \times 10^{-3} \ \mathrm N \end{align*}
具体例 2.3
50°C の水の表面張力を求めよ.
ただし, 25°C での水の表面張力は \(\gamma = 0.07199 \, \mathrm{N \, m^{-1}}\), \(\partial \gamma/\partial T = -15.6 \times 10^{-5} \, \mathrm{N \, m^{-1} \, K^{-1}}\) とする.
解答例 2.3
\begin{align*} \gamma (50 {}^\circ \mathrm C) & = (0.07199) + (-15.6 \times 10^{-5})(50 - 25) \\ & = 0.06809 = 0.0681 \ \mathrm {N \ m^{-1}} \end{align*}
表面張力の分子レベルでの理解
表面の分子は, エネルギー的に不安定.
\(\gamma\) は, 分子を液体の内部から表面に移動させ, 新たな表面をつくるのに必要なエネルギー
具体例 2.4
蒸発熱 \(\Delta_\mathrm{vap} U = 30.5 \, \mathrm{kJ \, mol^{-1}}\) (25°C)を用いて, シクロヘキサンの表面張力を評価せよ.
ただし, シクロヘキサンの密度は \(\rho = 773 \, \mathrm{kg \, m^{-3}}\), 分子量は \(M = 86.16 \, \mathrm{g \, mol^{-1}}\) とする.
計算を単純化するため, シクロヘキサンの液体は立方構造をとる(分子が立方格子状にならんでいる)とする.
立方構造では, 6 個の最近接分子がある.
表面では, 一つの最近接分子が欠けている(一つの結合が欠けている)ため, 「モルあたりの表面張力」は, \(\Delta_\mathrm{vap} U / 6 = 5.08 \, \mathrm{kJ \, mol^{-1}}\) と評価できる.
単位格子の 1 辺の長さを評価せよ.
表面張力を評価せよ.
解答例 2.4
\begin{align*} a_\mathrm M^3 & = \frac{M}{\rho N_\mathrm A} = \frac{(0.08416 \ \mathrm{kg \ mol^{_1}}}{(733 \ \mathrm{kg m^{-3}})(6.02 \times 10^{23} \ \mathrm {mol^{-1}})} \\ & = 1.81 \times 10^{-28} \ \mathrm{m^3} \\ a_\mathrm M & = 5.65 \times 10^{-10} \ \mathrm {m} \end{align*}
\begin{align*} \gamma & = \frac{\Delta_\mathrm{vap} U}{6 N_\mathrm A a^2_\mathrm M} \\ & = \frac{(30.5 \times 10^3) \ \mathrm{ J \ mol^{-1}}}{(6)(6.02\times10^{23} \ \mathrm{mol^{-1}})(0.565 \times 10^{-9} \mathrm m)^2 } \\ & = 0.0264 \ \mathrm{J \ m^{-2}} \end{align*}
具体例 2.5
水銀(\(25^\circ\mathrm C\)): \(485.48 \, \mathrm{mN \, m^{-1}}\)
ガリウムの溶融体(\(29.8^\circ\mathrm C\)): \(708 \, \mathrm{mN \, m^{-1}}\)
ニッケル(\(T_\mathrm m 1455^\circ\mathrm C\)): \(1780 \, \mathrm{mN \, m^{-1}}\)
鉄(\(T_\mathrm m 1538^\circ\mathrm C\)): \(1940 \, \mathrm{mN \, m^{-1}}\)
水性ゼラチンとデキストランの溶液 \(0.5 \, \mathrm{\mu N \, m^{-1}}\)
2.3 ヤング・ラプラス方程式
平均曲率と圧力差
界面の両側の圧力差は平均曲率に比例する.
球の場合,
平均曲率
平均曲率 \(R_\mathrm m\) は, 直交する2つの交線の曲率 \(R_1\), \(R_2\) によって次のように定義される.
式 (2.6) の右辺の括弧内 \(\times\) 1/2
曲面上のある点において, 直交する 2 つの交線をどの方向(:math:`360^circ`)にとっても, 平均曲率は変わらない (幾何学的にきまる量である).
cf. ガウス曲率
具体例 2.6
水中にできた直径 2 mm と 20 nm の泡を考える.
外部の圧力に対して内部の圧力はそれぞれ, どれだけ高くなるか.
解答例 2.6
\begin{align*} \Delta P & = \frac{2\gamma}{R} = \frac{(2)(0.072)}{1 \times 10^{-3}} = 144 \ \mathrm{Pa} \end{align*}
\begin{align*} \Delta P & = \frac{2\gamma}{R} = \frac{(2)(0.072)}{10 \times 10^{-9}} = 1.44 \times 10^7 \ \mathrm{Pa} \end{align*}
ヤング・ラプラス方程式の物理的意味
形から曲率がわかり, 圧力差が評価できる.
外場がない状況では, 液体表面の曲率は, どこでも同じ.
平衡状態の液体表面の形状の計算ができる.
表面の形状
簡単な形状以外は解析解を求めるのは難しい.
複雑な形状の場合, 接触角も含め, 数値的に(コンピューターで)求める.
ヤング・ラプラス方程式の導出(略)
ヤング・ラプラス方程式の応用
具体例 2.7
凸と凹の曲率をもつ表面
図 2.7 (b)
粒子の間にできるリング
毛管定数
\(\rho\): 密度 \(\mathrm{[kg~m^{-3}]}\)
\(g\): 重力加速度 \(\mathrm{[m~s^{-2}]}\)
\(h\): 高さ \(\mathrm{[m]}\)
\(\kappa\) の次元 (dimension) は長さである.
\(\kappa\) は物質の性質である.
\(R \ll \kappa\) の場合, 重力の影響は無視できる.
2.4 表面張力をはかる手法
手法の例
液滴法
ペンダント・ドロップ法
ペンダント・バブル法
セシル・バブル法
毛管上昇法
液滴重量法
円形張力計
ウィルヘルミープレート法
動的計測法
2.5 ケルビン方程式
表面の曲率が蒸気圧に及ぼす影響
液面が凸: (平衡)蒸気圧が増加
液面が凹: (平衡)蒸気圧が減少
ケルビン方程式
\(P_0\): 平坦表面からの蒸気圧 \(\mathrm{[Pa]}\)
\(P_0^\mathrm K\): 曲率をもった液体表面からの蒸気圧 \(\mathrm{[Pa]}\)
\(V_\mathrm m\): 液体のモル体積 \(\mathrm{[kg \ mol^{-1}]}\)
ここで, 半径はは液面が凸のときに正, 凹のときに負であるとする.
半径 \(r\) の球形の液滴
\[RT \ln \frac{P_0^\mathrm K}{P_0} = \frac{2 \gamma V_\mathrm m}{r} \tag{2.21a}\]または
\[P_0^\mathrm K = P_0 e^{\frac{2\gamma V_\mathrm m}{RTr}} = P_0 e^{\lambda_\mathrm K / r} \tag{2.21b}\]
ケルビン長
式 (2.20) より
左辺は蒸気圧の比の対数: 無次元
\((1/ R_1 + 1/R_2)\) は \(1 / \textsf{長さ}\) の次元, よって \(\lambda_\mathrm K\) は長さの次元をもつ.
\(r = 2 \lambda_\mathrm K\) のとき, 蒸気圧が \(\mathrm e\) 倍になる.
ケルビン長は物質の性質である.
\(\boxed{\textsf{曲率半径}=1/\textsf{曲率} \gg \lambda_\mathrm K}\) のとき, 蒸気圧変化は無視できる.
具体例 2.8
25°C でのケルビン長を水, エタノール, 1, 2-プロパンジオール(\(\mathrm{C_3H_8O_2}\))に関して計算せよ.
分子量はそれぞれ, \(M= 18.02, \ 46.07, \ 76.09 \ \mathrm{g \, mol^{-1}}\).
密度は, \(\rho = 997, \ 789, \ 1036 \, \mathrm{kg \, m^{-3}}\)
表面張力は, \(\gamma = 0.072, \ 0.02277, \ 0.04131 \, \mathrm{N \, m^{-1}}\)
1, 2-プロパンジオールの 298 K における表面張力のデータ例として \(0.04131 \ \mathrm{N \ m^{-1}}\) (Khattab et al. (2017))
解答例 2.8
\begin{align*} \lambda_\mathrm K (\text{water}) & = \frac{(0.072)\left(\frac{0.01802}{997}\right)}{(8.314)(298)} \\ &= 5.252497 \times 10^{-10} \ \mathrm{m} = 0.53 \ \mathrm{nm} \end{align*}
\begin{align*} \lambda_\mathrm K (\text{ethanol}) & = 5.20136 \times 10^{-10} = 0.52 \ \mathrm{nm} \tag{2.23} \end{align*}
\begin{align*} \lambda_\mathrm K (\mathrm{C_3H_8O_2}) & = 1.224607 \times 10^{-9} = 1.22 \ \mathrm{nm} \end{align*}
ケルビン方程式の導出
モル体積一定の仮定のもとに
気相中の液滴
オストワルド熟成
ある蒸気圧に対して, 液滴の臨界サイズが存在する.
核形成サイト
液中の気泡
表 2.2 半径 \(r\) の球形の水滴または泡に対する, 曲率をもった水表面の 25°C での相対平衡蒸気圧 \(P_0^\mathrm K / P_0\)
r (nm) |
液滴 |
泡 |
|---|---|---|
1000 |
1.001 |
0.999 |
100 |
1.011 |
0.989 |
10 |
1.114 |
0.898 |
1 |
2.950 |
0.339 |
第 3 列は 1/(第 2 列)
毛管凝縮が効いてくるのは, 曲率半径が数十 nm のオーダー
2.6 毛管凝縮
毛管凝縮とは
曲面での表面張力の影響で, 飽和蒸気圧以下でも液体が凝縮する現象
円錐形の完全に濡れ性の細孔に対して
参考: スリット状の完全に濡れ性の細孔(曲率半径の一つは無限大)
具体例 2.9
様々なサイズの細孔を持つ多孔質固体を考える.
関係湿度 90%, 温度 20°C とする.
表面が完全に濡れ性の場合, どのサイズの細孔までが水で満たされるか.
この条件下で, \(V_\mathrm m = 18 \times 10^{-6} \, \mathrm m^3\) とする.
解答例 2.9
式 (2.29) を変形して
\begin{align*} r &= - \frac{2 \gamma V_\mathrm m}{RT \ln \left(\frac{P_0^\mathrm K}{P_0} \right)} = -\frac{(2)(0.072)(18 \times 10^{-6})}{(8.314)(293)\ln(0.9)} \\ & = 1.0 \times 10^{-8} \ \mathrm{m} \end{align*}
毛管凝縮による粒子の付着
引力 \(\pi x^2 \Delta P\)
これを変形して最終的に
具体例 2.10
水晶球が他の水晶球にぶら下がっている.
室内には水蒸気が存在し, 毛管力が生じている.
小さな球は毛管力で保持され, 大きな球は重力により落下する.
重力と毛管力が釣り合うときの球の半径はいくらか.
水晶の密度は \(\rho = 3000 \ \mathrm{kg \, m^{-3}}\) とする.
解答例 2.10
球の重力は
毛管力は
このふたつが等しいとき
これより
2.7 核形成理論
均一核形成と不均一核形成
均一核形成: 表面が存在しないところで, まず小さな分子クラスターが形成され, 成長し, クラスター同士が凝集し, さらに成長する.
実際には, ほとんどの場合の核形成は, ほこりなどの不純物の表面上に凝集することで起こる不均一核形成である.
蒸発のギブズエネルギー
式 (2.35) の導出
過飽和蒸気からの液滴形成(均一核形成)
液滴の形成に必要なギブズエネルギー
凝集によるギブズエネルギー変化
表面積 \(A\) の液滴表面を形成するのに必要な仕事
ここで, 分子数 \(n = 4\pi r^3 / (3 V_\mathrm m)\), 表面積 \(A = 4 \pi r^2\) を代入
液滴を半径 \(r\) の完全な球と考え,\(V_{\mathrm m}\) をモル体積とすると,
臨界液滴半径 \(r^*\) は, \(\frac{\partial G}{\partial r} = 0\) より
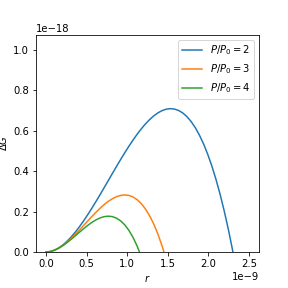
図 2.17 水蒸気が水滴へ凝縮する際のギブズエネルギー
具体例 2.11
0°C の水で, 過飽和度 \(P/P_0 = 4\) の場合を考える.
臨界半径 \(r^*\) を求めよ.
このようなクラスターをつくる最大ギブズ自由エネルギーを求めよ.
ただし, 0°C における水の表面張力を \(0.0756 \ \mathrm{N \, m^{-1}}\) とする.
臨界における液滴は, 約 70 分子の水に相当する.
解答例 2.11
式 (2.41) に \(P/P_0 = 4\), \(\gamma = 0.0756\), \(T = 273\), \(R=8.314\) を代入.
\begin{align*} r^* &= \frac{(2)(1.8 \times 10^{-5})(0.0756)}{(8.314)(273)\ln(4)} = 8.6496030 \times 10^{-10} \\& = 8.6 \ \times 10^{-10} \mathrm{m} \end{align*}
式 (2.40) に \(P/P_0 = 4\), \(r = r^* = 8 \times 10^{10} \ \mathrm m\), \(V_\mathrm m = 1.8 \times 10^{-5}\) 等を代入
\begin{align*} &\frac{(4 \pi)(8.314)(273)(r^*)^3 \ln(4)}{(3)(1.8 \times 10^{-5})} + 4 \pi (0.0756)(r^*)^2 \\ & = 2.3692056 \times 10^{-19} \\ & = 2.4 \times 10^{-19} \ \mathrm J \end{align*}
教科書では \(\Delta G_\mathrm{max} = 1.9 \times 10^{-19} \ \mathrm J\) となっているが, ここでの計算では, \(\Delta G_\mathrm{max} = 2.4 \times 10^{-19} \ \mathrm J\) となった.
具体例 2.12
膨張型チャンバーを用いて水の核形成を調べる.
初期条件 \(2330~\mathrm{Pa}\), \(303~\mathrm{K}\) の蒸気を膨張させ, 圧力を \(1575~\mathrm{Pa}\) まで下げる.
\(260~\mathrm K\) での平衡蒸気圧は, \(219~\mathrm{Pa}\) であり, 過飽和度は \(P/P_0 = 7.2\) となる.
この場合の核形成速度はいくらか.
解答例 2.12
\(260~\mathrm K\) での水の表面張力は, \(0^\circ\mathrm C\) 以上での値を外挿することで, \(\gamma \approx 77~\mathrm{mN \, m^{-1}}\) と求められる.
分子体積は, \(v_\mathrm m = m /\rho = 2.99\times 10^{-29}~\mathrm{m^3}\) と計算できる. ここで, \(m\) は水の質量である.
\begin{align*} J & = \sqrt{\frac{20.077}{\pi(2.99 \times 10^{-26})}}(2.99 \times 10^{-29})\left(\frac{1575}{3.59\times 10^{-21}} \right) \\ & \quad \times \exp \left\{\frac{16 \pi (2.99 \times 10^{-29})^2(0.077)^3}{(3)(3.59\times 10^{-21})^3 \ln^2 7.2} \right\} \\ & = 2.54 \times 10^{14} \mathrm{s^{-1}~m^{-3}} \end{align*}
[1]:
#### 2.1
import numpy as np
kb = 1.380649e-23
m = 3e-26
tt = 298
p = 3168
a = 10e-20
v = p * a / np.sqrt(2 * np.pi * m * kb * tt)
t = 1 / v
print('v = {:.7e}'.format(v))
print('t = {:.7e}'.format(t))
v = 1.1375876e+07
t = 8.7905321e-08
[2]:
#### 2.2
2 * 72e-3 * 0.01
[2]:
0.0014399999999999999
[3]:
#### 2.3
0.07199 - (15.6e-5 * 25)
[3]:
0.06809
[4]:
#### 2.4
a3 = 0.08416 / 773 / 6.02e23
a = a3**(1/3)
gamma = 5080 / 6.02e23 / 0.565e-9**2
print(a3)
print(a)
print(gamma)
1.8085467587558503e-28
5.655138519702248e-10
0.026434452834145403
[5]:
#### 2.6
print('{:.2e}'.format(0.072 * 2 / 10e-9))
1.44e+07
[6]:
#### 2.8
lambda_water = 0.072 * (0.01802/997) / 8.314 / 298
lambda_ethanol = 0.02207 * (0.04607/789) / 8.314 / 298
lambda_c3h8o2 = 0.04131 * (0.07609 / 1036) /8.314/ 298
print(lambda_water)
print(lambda_ethanol)
print(lambda_c3h8o2)
5.252497332454067e-10
5.201364125497927e-10
1.2246070051756427e-09
[7]:
#### 2.9
import numpy as np
res = 2 * 0.072 * 18e-6 / 8.314/ 293 / np.log(0.9)
print(res)
-1.009902550902237e-08
[8]:
#### 2.10
import numpy as np
g = 9.81
rho = 3000
gamma = 0.072
c1 = 4 / 3 * np.pi * rho * g
c2 = 2 * np.pi * gamma
rc = (c2 / c1)**0.5
print("{:.7e}".format(c1))
print("{:.7e}".format(c2))
print("{:.7e}".format(rc))
1.2327610e+05
4.5238934e-01
1.9156526e-03
[9]:
#### 2.11
import numpy as np
# V_m = M / rho
rho = 1000
v_m = 18e-3 / rho
rr = 8.314
tt = 273
gamma = 0.0756
rc = 2 * v_m * gamma / rr / tt /np.log(4)
dg = - 4 / 3 * np.pi * rr * tt * rc**3 / v_m * np.log(4) + 4 * np.pi * gamma * rc**2
print('r* = {:.7e}'.format(rc))
print('Delta G = {:.7e}'.format(dg))
r* = 8.6496030e-10
Delta G = 2.3692056e-19
| ◀ Previous | TOC | Next ▶ |